选修4-4:坐标系与参数方程
已知曲线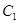 的参数方程为
的参数方程为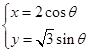 (
(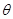 为参数),以坐标原点
为参数),以坐标原点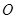 为极点,
为极点,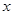 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线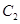 的极坐标方程为
的极坐标方程为
(1)分别写出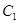 的普通方程,
的普通方程,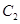 的直角坐标方程;
的直角坐标方程;
(2)已知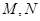 分别为曲线
分别为曲线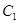 的上,下顶点,点
的上,下顶点,点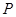 为曲线
为曲线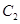 上任意一点,求
上任意一点,求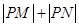 的最大值
的最大值
在 中,
中, 分别是
分别是 的对边长,已知
的对边长,已知 成等比数列,且
成等比数列,且 ,求
,求 的大小及
的大小及 的值.
的值.
已知函数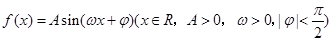 的图象(部分)如图所示.
的图象(部分)如图所示.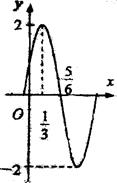
(1)试确定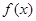 的解析式;
的解析式;
(2)若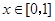 ,求函数
,求函数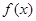 的值域.
的值域.
已知二次函数f(x)=x2+ax(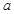
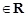 ).
).
(1)若函数y=f(sinx+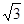 cosx)(
cosx)(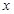
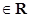 )的最大值为
)的最大值为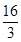 ,求f(x)的最小值;
,求f(x)的最小值;
(2)当a>2时,求证:f(sin2xlog2sin2x+cos2xlog2cos2x)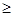 1–a.其中x∈R,x¹kp且x¹kp
1–a.其中x∈R,x¹kp且x¹kp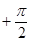 (k∈Z).
(k∈Z).
已知函数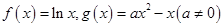 .
.
(1)若函数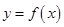 与
与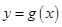 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数 的值及点P的坐标;
的值及点P的坐标;
(2)若函数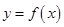 与
与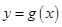 的图象有两个不同的交点M、N,求实数
的图象有两个不同的交点M、N,求实数 的取值范围 .
的取值范围 .
在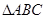 中,满足:
中,满足: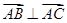 ,
,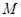 是
是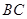 的中点.
的中点.
(1)若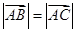 ,求向量
,求向量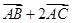 与向量
与向量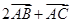 的夹角的余弦值;
的夹角的余弦值;
(2)若点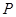 是
是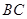 边上一点,
边上一点,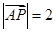 ,且
,且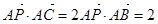 ,求
,求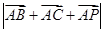 的最小值.
的最小值.