如图，在平面直角坐标系
中，圆
交
轴于点
（点
在轴的负半轴上），点
为圆
上一动点，
分别交直线
于
两点。
（1）求两点纵坐标的乘积；
（2）若点
的坐标为
，连接
交圆于另一点
．
①试判断点与以
为直径的圆的位置关系，并说明理由；
②记
的斜率分别为
，试探究
是否为定值？若是，请求出该定值；若不是，请说明理由．
求y=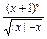
的定义域：
求证:经过平面外一点有且只有一个平面和已知平面平行
已知: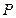
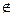α
求证:过点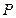有且只有一个平面β∥α
已知函数f(x)=logax(a＞0,a≠1)，如果对于任意x∈［3，+∞）都有|f(x)|≥1成立，
试求a的取值范围.
已知定义在R上的奇函数f(x)有最小正周期2，且当x∈(0,1)时，f(x)=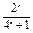
.
（1）求f（x)在［-1，1］上的解析式；（2）证明：f(x)在（0，1）上是减函数.
已知函数f(x),当x,y∈R时，恒有f(x+y)=f(x)+f(y).（1）求证：f(x)是奇函数；
（2）如果x∈R+，f（x）＜0,并且f(1)=-
,试求f(x)在区间［-2，6］上的最值.