已知| |=3,|
|=3,| |=5,
|=5, 与
与 的夹角为120°.
的夹角为120°.
试求:(1) ;
;
(2) ;
;
(3) .
.
(本题12分)在2008年北京奥运会青岛奥帆赛举行之前,为确保赛事安全,青岛海事部门举行奥运安保海上安全演习.为了测量正在海面匀速行驶的某航船的速度,在海岸上选取距离为1千米的两个观察点C,D,在某天10:00观察到该航船在A处,此时测得∠ADC=30°,3分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,求船的速度是多少千米/分钟.
(本题12分)如图,已知AD为⊙O的直径,直线BA与⊙O相切于点A,直线OB与弦AC垂直并相交于点G.
求证:BA·DC=GC·AD.
.(本题12分)已知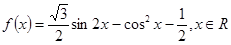 .
.
⑴化简并求函数的最小正周期
⑵求函数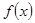 的最大值,并求使
的最大值,并求使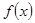 取得最大值的
取得最大值的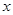 的集合
的集合
(本题12分)设函数
⑴求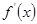 的表达式;
的表达式;
⑵求 的单调区间、极大值、极小值。
的单调区间、极大值、极小值。
(本题12分)如右图,在三角形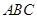 中,
中,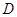 ,
,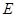 分别为
分别为 ,
,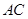 的中 点,
的中 点,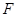 为
为 上的点,且
上的点,且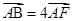 . 若
. 若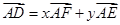 ,求实数
,求实数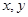 。
。