已知函数f(x)=sinxcosx﹣cos2x.
(1)求f(x)的最小正周期;
(2)求f(x)在区间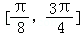 上的最小值,并求取得最小值时x的值.
上的最小值,并求取得最小值时x的值.
已知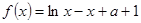
(1)若存在 使得
使得 ≥0成立,求
≥0成立,求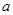 的范围
的范围
(2)求证:当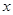 >1时,在(1)的条件下,
>1时,在(1)的条件下, 成立
成立
已知椭圆中心在原点,焦点在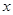 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为
(1)求椭圆的方程;
(2)设直线 经过点
经过点 (0,1),且与椭圆交于
(0,1),且与椭圆交于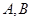 两点,若
两点,若 ,求直线
,求直线 的方程.
的方程.
已知梯形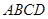 中
中 ,
,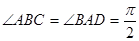 ,
,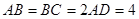 ,
,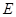 、
、 分别是
分别是 、
、 上的点,
上的点,
 ,
,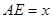 .沿
.沿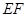 将梯形
将梯形 翻折,使平面
翻折,使平面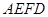 ⊥平面
⊥平面 (如图).
(如图).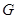 是
是 的中点.
的中点.
(1)当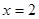 时,求证:
时,求证: ⊥
⊥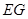 ;
;
(2)当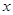 变化时,求三棱锥
变化时,求三棱锥 体积的最大值.
体积的最大值.
某年青教师近五年内所带班级的数学平均成绩统计数据如下:
年份 年 年 |
2009 |
2010 |
2011 |
2012 |
2013 |
平均成绩 分 分 |
97 |
98 |
103 |
108 |
109 |
(1)利用所给数据,求出平均分与年份之间的回归直线方程 ,并判断它们之间是正相关还是负相关。
,并判断它们之间是正相关还是负相关。
(2)利用(1)中所求出的直线方程预测该教师2014年所带班级的数学平均成绩.



在 中,
中,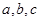 分别为内角A,B,C所对的边长,
分别为内角A,B,C所对的边长, ,
,
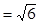 .
.
(1)求角B的大小。
(2)若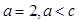 求
求 的面积
的面积 .
.