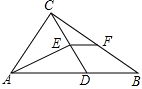
(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求线段MN的长度.
(2)对于(1)问,如果我们这样叙述:“已知点C在直线AB上,且AC=6cm,BC=4cm,点M、N分别是AC,BC的中点,求线段MN的长度.”结果会有变化吗?如果有,求出结果;如果没有,说明理由.
求下列各数的算术平方根:
(1)625;(2)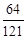 ;(3)
;(3)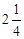 ;(4)2.89.
;(4)2.89.
如图,△ABC中,AD为∠BAC的平分线,点F是BC的中点,BP⊥AD于D,AC=12,AB=8,求PF的长.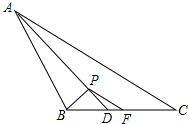
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,阅读下列材料,
(1)连接AC、BD,由三角形中位线的性质定理可证四边形EFGH是________;
(2)对角线AC、BD满足条件_______时,四边形EFGH是矩形;
(3)对角线AC、BD满足条件_______时,四边形EFGH是菱形;
(4)对角线AC、BD满足条件_________时,四边形EFGH是正方形.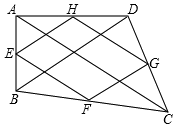
如图,在△ABC中,AD为角平分线,CE⊥AD,F为BC中点.
求证:EF=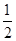 (AB-AC).
(AB-AC).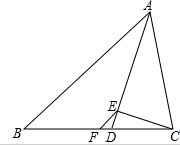
如图,在△ABC中,D是AB上一点,且AD=AC,AE⊥CD,垂足是E,F是CB的中点.求证:BD=2EF.