已知数轴上有A、B、C三点,分别代表﹣24,﹣10,10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.

(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是 .
如图,△ABC中,∠B=50°,AD平分∠BAC, ∠ADC=80°,求∠C的度数。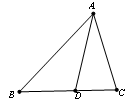
锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,(y>0).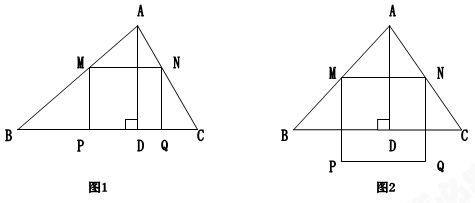
(1)△ABC中边BC上高AD= _______;
(2)当x= _______时PQ恰好落在边BC上(如图1);
(3)当PQ在△ABC外部时(如图2),求y关于x的函数关系式,并求出z为何值时y
最大,最大值是多少?1
如图,反比例函数y= 的图象与直线y=x+m在第一象限交于点P(6,2),A、B为直线上的两点,点A的横坐标为2,点B的横坐标为3.D、C为反比例函数图象上的两点,且AD、BC平行于y轴。
的图象与直线y=x+m在第一象限交于点P(6,2),A、B为直线上的两点,点A的横坐标为2,点B的横坐标为3.D、C为反比例函数图象上的两点,且AD、BC平行于y轴。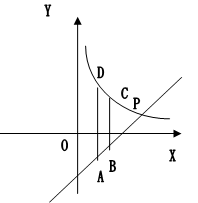
(1) 求反比例函数y= 与直线y=x+m的函数关系式
与直线y=x+m的函数关系式
(2)求梯形ABCD的面积.
A、B、C、D、E五位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一次比赛.
(1)请用画树状图或列表法,求恰好选中A、B两位同学的概率;
(2)若已确定A打第一场,再从其余四位同学中随机选取一位,求恰好选中B同学的概率.
小刘对本班同学的业余兴趣爱好进行了一次调查,她根据采集到的数据,绘制了下面的图1 和图2.请你根据图中提供的信息,解答下列问题:
(1)在图1中,将“书画”部分的图形补充完整;
(2)在图2中,求出“球类’’部分所对应的圆心角的度数,并分别写出爱好“音乐”、“书画”的人数占本班学生数的百分数;