用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面; B方法:剪4个侧面和5个底面.

现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,工厂需要一次性投入机器租赁、安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱 个,请分别写出从纸箱厂购买纸箱的费用y(元)和蔬菜
个,请分别写出从纸箱厂购买纸箱的费用y(元)和蔬菜加工厂自己加工制作纸箱的费用y2(元)关于 (个)的函数关系式;
(个)的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
小明受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作:

请根据图中给出的信息,解答下列问题:
(1)放入一个小球量筒中水面升高_______cm;
(2)求放入小球后量筒中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式(不要求写出自变量的取值范围);
(3)量筒中至少放入几个小球时有水溢出?
已知:y-1与x+2成正比例,且x=1时,y=4.
(1)写出 与
与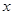 之间的函数关系式;
之间的函数关系式;
(2)在图中画出此函数的图像;
(3) 求此直线与坐标轴围成的三角形的面积.
(4)观察图像,直接写出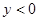 时
时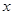 的取值范围.
的取值范围.
已知直线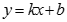 经过点
经过点 ,
, .
.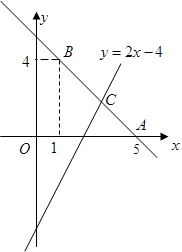
(1)求直线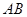 的解析式;
的解析式;
(2)若直线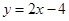 与直线
与直线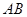 相交于点
相交于点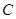 ,求点
,求点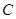 的坐标;
的坐标;
(3)根据图象,直接写出关于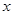 的不等式
的不等式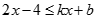 的解集.
的解集.
已知:如图,点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.
求证:(1)△ABC≌△DEF;
(2)BE=CF.