在平面直角坐标系 中,点 的坐标为 , ,点 的坐标为 , ,且 , ,若 , 为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点 , 的"相关矩形",如图为点 , 的"相关矩形"示意图.
(1)已知点 的坐标为 ,
①若点 的坐标为 ,求点 , 的"相关矩形"的面积;
②点 在直线 上,若点 , 的"相关矩形"为正方形,求直线 的表达式;
(2) 的半径为 ,点 的坐标为 ,若在 上存在一点 ,使得点 , 的"相关矩形"为正方形,求 的取值范围.

在一个可以改变体积的容器内有一定质量的二氧化碳气体,当改变容器的体积时,气体的密度也会随之改变,密度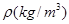 与体积
与体积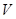
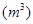 之间的函数关系如图所示,。
之间的函数关系如图所示,。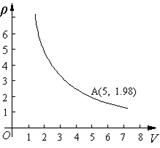
(1)通过图象你能得到什么信息(至少写一条)?
(2)写出 与
与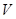 之间函数关系式;
之间函数关系式;
(3)求当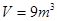 时,二氧化碳的密度
时,二氧化碳的密度 。
。
先化简代数式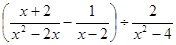 ,请你取一个
,请你取一个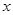 的值,求出此时代数式的值.
的值,求出此时代数式的值.
如图,经过原点的抛物线 与
与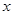 轴的另一个交点为A.过点
轴的另一个交点为A.过点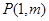 作直线
作直线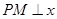 轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP。
轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP。当
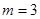 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;当
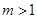 时,连结CA,问
时,连结CA,问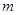 为何值时
为何值时 ?
?过点P作
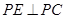 且
且 ,问是否存在
,问是否存在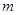 ,使得点E落在坐标轴上?若存在,求出所有满足要求的
,使得点E落在坐标轴上?若存在,求出所有满足要求的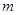 的值,并定出相对应的点E坐标;若不存在,请说明理由。
的值,并定出相对应的点E坐标;若不存在,请说明理由。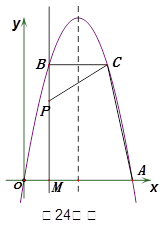
温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将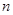 件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示。设安排
件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示。设安排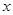 件产品运往A地。
件产品运往A地。当
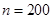 时①根据信息填表:
时①根据信息填表:
| A地 |
B地 |
C地 |
合计 |
|
| 产品件数(件) |
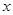 |
 |
200 |
|
| 运费(元) |
30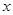 |
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?若总运费为5800元,求
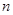 的最小值。
的最小值。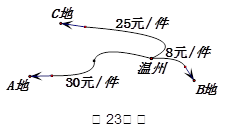
如图,△ABC中,∠ACB=90°,D是边AB上的一点,且∠A=2∠DCB.E是BC上的一点,以EC为直径的⊙O经过点D。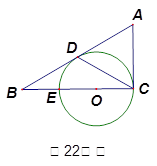
求证:AB是⊙O的切线;
若CD的弦心距为1,BE=ED.求BD的长.