为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 |
|||||
出行方式 |
共享单车 |
步行 |
公交车 |
的士 |
私家车 |
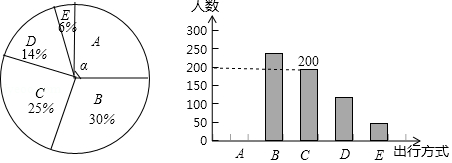
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择类的人数有 人;
(2)在扇形统计图中,求类对应扇形圆心角的度数,并补全条形统计图;
(3)该市约有12万人出行,若将,,这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
在边长为1的正方形网格中,正方形 与正方形
与正方形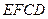 的位置如图所示.
的位置如图所示.
(1)请你按下列要求画图:
① 联 结
结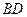 交
交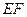 于点
于点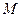 ;
;
② 在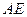 上取一点
上取一点 ,联结
,联结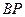 ,
,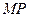 ,使△
,使△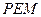 与△
与△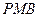 相似;
相似;
(2)若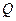 是线段
是线段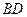 上一点,连结
上一点,连结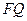 并延长交四边形
并延长交四边形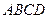 的一边于点
的一边于点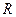 ,且满足
,且满足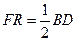 ,则
,则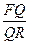 的值为______
的值为______ _______.
_______.
远洋电器城中,某品牌电视有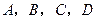 四种不同型号供顾客选择,它们每
四种不同型号供顾客选择,它们每
台的价格(单位:元)依次分别是:2500,4000,6000,10000.为做好下阶段的销售工作,
商场调查了一周内这四种不同型号 电视的销售情况,并根据销售情况,将所得的数据制成
电视的销售情况,并根据销售情况,将所得的数据制成
统计图,现已知该品牌一周内四种型号电视共售出240台,每台的销售利润占其价格的百分
比如下表:
| 型号 |
A |
B |
C |
D |
| 利润 |
10% |
12% |
15% |
20% |
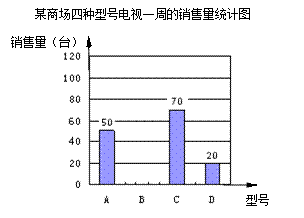
请根据以上信息,解答下列问题:
(1)请补全统计图;
(2)通过计算,说明商场这一周内该品牌哪种型号 的电视总销售利润最大;
的电视总销售利润最大;
(3)谈谈你的建议.
已知:如图,在矩形 中,点
中,点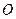 在对角线
在对角线 上,以
上,以 的长为半径的⊙
的长为半径的⊙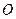
与 ,
, 分别交于点E、点F,且∠
分别交于点E、点F,且∠ =∠
=∠ .
.
(1)判断直线 与⊙
与⊙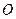 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(2)若 ,
, ,求⊙
,求⊙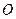 的半径.
的半径.
已知:如图,直角梯形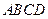 中,
中,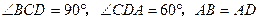 ,
,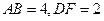 ,求
,求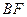
 的长.
的长.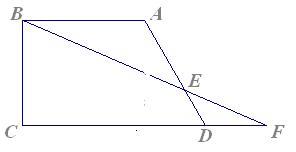
为继续进行旅游景区公共服务改造,某市今年预算用资金41万元在200余家A
级景区配备两 种轮椅1100台,其中普通轮椅每台360元,轻便型轮椅每台500元.
种轮椅1100台,其中普通轮椅每台360元,轻便型轮椅每台500元.
(1) 若恰好全部用完预算资金,能购买 两种轮椅各多少台?
两种轮椅各多少台?
(2) 由于获得了不超过4万元的社会捐助,问轻便型轮椅最多可以买多少台?