如图,已知 的半径为5, 是 的内接三角形, ,.过点 作 的切线 ,过点 作 ,垂足为 .
(1)求证:
(2)求线段 的长.

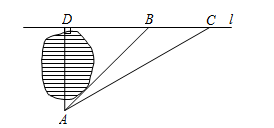
如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路. 现新修一条路AC到公路l. 小明测量出∠ACD=30º,∠ABD=45º,BC="50m." 请你帮小明计算他家到公路l的距离AD的长度(精确到0.1m;参考数据: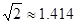 ,
,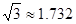 ).
).
某品牌瓶装饮料每箱价格26元.某商店对该瓶装饮料进行“买一送三”促销活动,若整箱购买,则买一箱送三瓶,这相当于每瓶比原价便宜了0.6元.问该品牌饮料一箱有多少瓶?
如图,在平面直角坐标系中,点P的坐标为(-4,0),⊙P的半径为2,将⊙P沿x轴向右平移4个单位长度得⊙P1.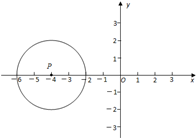
(1)画出⊙P1,并直接判断⊙P与⊙P1的位置关系;
(2)设⊙P1与x轴正半轴,y轴正半轴的交点分别为A,B,求劣弧AB与弦AB围成的图形的面积(结果保留π).π)
解不等式组: ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.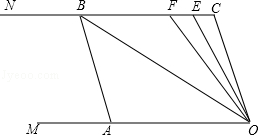
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.