已知：如图，DABC内接于⊙O，AB为直径，∠CBA的平分线交AC于点F，交⊙O于点D，DE⊥AB于点E，且交AC于点P，连结AD．
（1）求证：AP=PD；
（2）请判断A，D，F三点是否在以P为圆心，以PD为半径的圆上？并说明理由；
（3）连接CD，若CD﹦3，BD ﹦4，求⊙O的半径和DE的长．
如图，在⊙O中，∠ACB=∠BDC=60°，AC=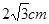
，
（1）判断△ABC的形状并证明你的结论；
（2）求⊙O的周长
在平面直角坐标系中，△ABC的顶点坐标是A（-7，1），B（1，1），C（1，7）．线段DE的端点坐标是D（7，-1），E（-1，-7）．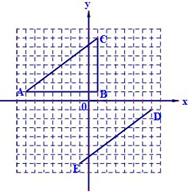
（1）试说明如何平移线段AC，使其与线段ED重合；
（2）将△ABC绕坐标原点O逆时针旋转，使AC的对应边为DE，请直接写出点B的对应点F的坐标；
（3）画出（2）中的△DEF，并和△ABC同时绕坐标原点O逆时针旋转90°，画出旋转后的图形.
如图所示，在一块长为32米，宽为15米的矩形草地上，在中间要设计一横二竖的供居民散步的小路，要使小路的面积是草地总面积的八分之一，请问小路的宽应是多少米？（注：所有小路进出口的宽度相等，且每段小路均为平行四边形）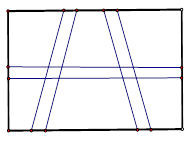
我们知道：对于任何实数
，①∵
≥0，∴+1＞0；②∵
≥0，∴+
＞0.
模仿上述方法解答：
求证：（1）对于任何实数，均有：
＞0；
（2）不论为何实数，多项式
的值总大于
的值．
