如图,海中有两个小岛,,某渔船在海中的处测得小岛位于东北方向上,且相距,该渔船自西向东航行一段时间到达点处,此时测得小岛恰好在点的正北方向上,且相距,又测得点与小岛相距.
(1)求的值;
(2)求小岛,之间的距离(计算过程中的数据不取近似值).
已知一元二次方程 的一根为2.
的一根为2.
(1)求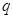 关于
关于 的关系式;
的关系式;
(2)若 ,求方程的另一根;
,求方程的另一根;
(3)求证:抛物线 与
与 轴有两个交点.
轴有两个交点.
菜农李伟种植的某蔬菜计划以每千克5元的单价对外批发销售,由于部分菜农盲目扩大
种植,造成该蔬菜滞销.李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克3.2元的单价对外批发销售.
(1)求平均每次下调的百分率;
(2)小华准备到李伟处购买5吨该蔬菜,因数量多,李伟决定再给予两种优惠方案以供选择:
方案一:打九折销售;
方案二:不打折,每吨优惠现金200元.试问小华选择哪种方案更优惠,请说明理由.
在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法(或树状图)表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点(x,y)落在反比例函数 的图象上的概率;
的图象上的概率;
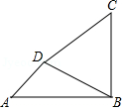
如图,在Rt△ABC中,∠C=90°.
(1)用直尺和圆规作△ABC的BC边上的垂直平分线,与AB交于D点,与BC交于E点(保留作图痕迹,不写作法);
(2)若AC=6,AB=10,连结CD,求DE=;CD=.
反比例函数y= 的图象经过点A(4,-2),
的图象经过点A(4,-2),
(1)求这个函数的解析式;
(2)请判断点B(1,8)是否在这个反比例函数的图象上,并说明理由.
(3)当1<x<2时,直接写出y 的取值范围: