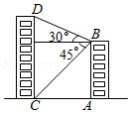
如图,在平面直角坐标系中,已知二次函数的图象经过点,,其对称轴为直线.
(1)求该二次函数的解析式;
(2)若直线将的面积分成相等的两部分,求的值;
(3)点是该二次函数图象与轴的另一个交点,点是直线上位于轴下方的动点,点是第四象限内该二次函数图象上的动点,且位于直线右侧.若以点为直角顶点的与相似,求点的坐标.

如图, , , , .
(1)求 的度数;
(2)若 ,求证: .
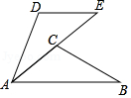
如图,是某小区的甲、乙两栋住宅楼,小丽站在甲栋楼房 的楼顶,测量对面的乙栋楼房 的高度.已知甲栋楼房 与乙栋楼房 的水平距离 米,小丽在甲栋楼房顶部 点,测得乙栋楼房顶部 点的仰角是 ,底部 点的俯角是 ,求乙栋楼房 的高度(结果保留根号).
先化简,再求值: ,其中 .
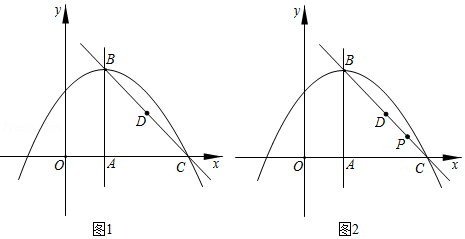
如图1,抛物线 经过点 ,顶点为 ,对称轴 与 轴相交于点 , 为线段 的中点.
(1)求抛物线的解析式;
(2) 为线段 上任意一点, 为 轴上一动点,连接 ,以点 为中心,将 逆时针旋转 ,记点 的对应点为 ,点 的对应点为 .当直线 与抛物线 只有一个交点时,求点 的坐标.
(3) 在(2)的旋转变换下,若 (如图 .
①求证: .
②当点 在(1)所求的抛物线上时,求线段 的长.
如图1, 是 的直径,直线 与 相切于点 ,直线 与 相切于点 ,点 (异于点 在 上,点 在 上,且 ,延长 与 相交于点 ,连接 并延长交 于点 .
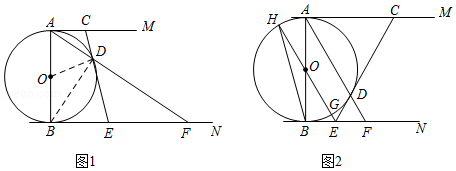
(1)求证: 是 的切线;
(2)求证: ;
(3)如图2,连接 并延长与 分别相交于点 、 ,连接 .若 , ,求 .