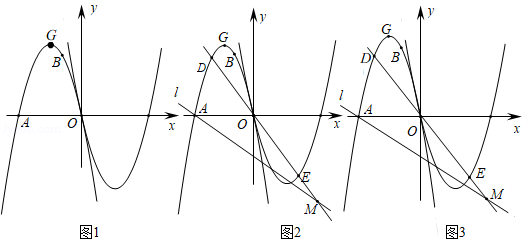
如图1，抛物线经过点、两点，是其顶点，将抛物线绕点旋转，得到新的抛物线．
（1）求抛物线的函数解析式及顶点的坐标；
（2）如图2，直线经过点，是抛物线上的一点，设点的横坐标为，连接并延长，交抛物线于点，交直线于点，若，求的值；
（3）如图3，在（2）的条件下，连接、，在直线下方的抛物线上是否存在点，使得？若存在，求出点的横坐标；若不存在，请说明理由．
如图，C、F在BE上，∠A=∠D，AB∥DE，BF=EC．
求证：AB=DE．
如图,∠ABC=∠BCD,∠1=∠2,请问图中有几对平行线？并说明理由.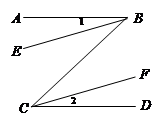 
如图，在平面直角坐标系xOy中，⊙C的圆心坐标为（－2，－2），半径为
．函数y＝－x＋2的图象与x轴交于点A，与y轴交于点B，点P为直线AB上一动点．
（1）若△POA是等腰三角形，且点P不与点A、B重合，直接写出点P的坐标；
（2）当直线PO与⊙C相切时，求∠POA的度数；
（3）当直线PO与⊙C相交时，设交点为E、F，点M为线段EF的中点，令PO＝t，MO＝s，求s与t之间的函数关系式，并写出t的取值范围．
在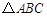
中，∠ACB=90°，AC＞BC，D是AC边上的动点，E是BC边上的动点，AD=BC，CD="BE" ．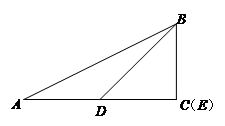
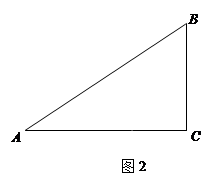
（1） 如图1，若点E与点C重合，连结BD，请写出∠BDE的度数；
（2）若点E与点B、C不重合，连结AE 、BD交于点F，请在图2中补全图形，并求出∠BFE的度数．
二次函数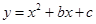
的图象如图所示，其顶点坐标为M(1,-4)．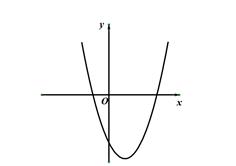
（1）求二次函数的解析式；
（2）将二次函数的图象在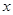
轴下方的部分沿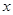轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合新图象回答：当直线
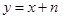与这个新图象有两个公共点时，求
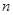的取值范围．