某商场准备购进、两种型号电脑，每台型号电脑进价比每台型号电脑多500元，用40000元购进型号电脑的数量与用30000元购进型号电脑的数量相同，请解答下列问题：
（1），型号电脑每台进价各是多少元？
（2）若每台型号电脑售价为2500元，每台型号电脑售价为1800元，商场决定同时购进，两种型号电脑20台，且全部售出，请写出所获的利润（单位：元）与型号电脑（单位：台）的函数关系式，若商场用不超过36000元购进，两种型号电脑，型号电脑至少购进10台，则有几种购买方案？
（3）在（2）问的条件下，将不超过所获得的最大利润再次购买，两种型号电脑捐赠给某个福利院，请直接写出捐赠，型号电脑总数最多是多少台．
已知：如图在梯形ABCD中，AD//BC，∠ABC=45o，∠ADC=120o，AD=DC，AB=2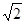
，求：BC的长。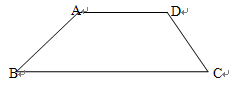
（本题12分）如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连结OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连结CF．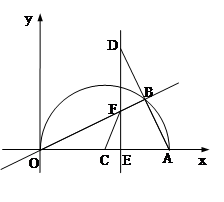
（1）当∠AOB=30°时，求弧AB的长度；
（2）当DE=8时，求线段EF的长；
（3）在点B运动过程中，当交点E在O，C之间时，是否存在以点E、C、F为顶点的三角形与△AOB相
似，若存在，请求出此时点E的坐标；若不存在，请说明理由．
（本题满分10分)有一种葡萄：从树上摘下后不保鲜最多只能存放一周，如果放在冷藏室，可以延长保鲜时间，但每天仍有一定数量的葡萄变质，假设保鲜期内的重量基本保持不变，现有一位个体户，按市场价收购了这种葡萄200千克放在冷藏室内，此时市场价为每千克2元，据测算，此后每千克鲜葡萄的市场价格每天可以上涨0．2元，但是，存放一天需各种费用20元，平均每天还有1千克葡萄变质丢弃．(1)存放x天后将鲜葡萄一次性出售，设鲜葡萄的销售金额为y元，写出y关于x的函数关系式；
(2)为了使鲜葡萄的销售金额为760元，又为了尽早清空冷藏室，则需要在几天后一次性出售完；
(3)问个体户将这批葡萄存放多少天后一次性出售，可获得最大利润?最大利润是多少?(本题不要求写出自变量x的取值范围)
(本题满分10分) 如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE＝∠B．
求证：△ADF∽△DEC；
若AB＝4，AD＝3
，AE＝3，求AF的长．
(本题满分9分) 如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．
(1)求证：AD⊥CD；
(2)若AD=2，AC=
，求AB的长．