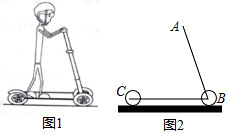
2020年2月,贵州省积极响应国家“停课不停学”的号召,推出了“空中黔课”.为了解某中学初三学生每天听空中黔课的时间,随机调查了该校部分初三学生.根据调查结果,绘制出了如图统计图表(不完整),请根据相关信息,解答下列问题:
部分初三学生每天听空中黔课时间的人数统计表
时间 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
人数人 |
2 |
6 |
6 |
10 |
4 |
(1)本次共调查的学生人数为 ,在表格中, ;
(2)统计的这组数据中,每天听空中黔课时间的中位数是 ,众数是 ;
(3)请就疫情期间如何学习的问题写出一条你的看法.
已知函数 , 为常数)的图象经过点 .
(1)求 , 满足的关系式;
(2)设该函数图象的顶点坐标是 ,当 的值变化时,求 关于 的函数解析式;
(3)若该函数的图象不经过第三象限,当 时,函数的最大值与最小值之差为16,求 的值.
我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于 ,可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.
(1)已知凸五边形 的各条边都相等.
①如图1,若 ,求证:五边形 是正五边形;
②如图2,若 ,请判断五边形 是不是正五边形,并说明理由:
(2)判断下列命题的真假.(在括号内填写“真”或“假”
如图3,已知凸六边形 的各条边都相等.
①若 ,则六边形 是正六边形;
②若 ,则六边形 是正六边形.
安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,将收集的数据制成如下统计图表.

(1)宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?
(2)该市约有30万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;
(3)小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.
如图1,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度 (单位: 与下行时间 (单位: 之间具有函数关系 ,乙离一楼地面的高度 (单位: 与下行时间 (单位: 的函数关系如图2所示.
(1)求 关于 的函数解析式;
(2)请通过计算说明甲、乙两人谁先到达一楼地面.

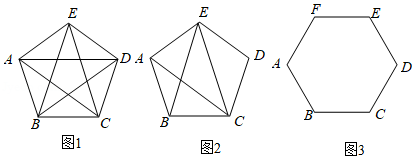
图1是一辆在平地上滑行的滑板车,图2是其示意图.已知车杆 长 ,车杆与脚踏板所成的角 ,前后轮子的半径均为 ,求把手 离地面的高度(结果保留小数点后一位;参考数据: , , .