遵义市各校都在深入开展劳动教育，某校为了解七年级学生一学期参加课外劳动时间（单位： 的情况，从该校七年级随机抽查了部分学生进行问卷调查，并将调查结果绘制成如下不完整的频数分布表和频数分布直方图．
课外劳动时间频数分布表：
劳动时间分组 |
频数 |
频率 |
|
2 |
0.1 |
|
4 |
|
|
6 |
0.3 |
|
|
0.25 |
|
3 |
0.15 |
解答下列问题：
（1）频数分布表中 ， ；将频数分布直方图补充完整；
（2）若七年级共有学生400人，试估计该校七年级学生一学期课外劳动时间不少于 的人数；
（3）已知课外劳动时间在 的男生人数为2人，其余为女生，现从该组中任选2人代表学校参加"全市中学生劳动体验"演讲比赛，请用树状图或列表法求所选学生为1男1女的概率．
如图，以线段AB为直径作⊙O，CD与⊙O相切于点E，交AB的延长线于点D， 连接BE，过点O作OC∥BE交切线DE于点C，连接AC ．
（1）求证：AC是⊙O的切线 ；
（2）若BD=OB=4，求弦AE的长．
在平面直角坐标系xoy中，直线y="-x+3" 与x轴、y轴分别交于A、B，在△AOB内部作正方形，使正方形的四个顶点都落在该三角形的边上，求正方形落在x轴正半轴的顶点坐标。
先化简，再求值．
，其中 x=tan600+2 ．
如图，矩形ABOD的两边OB，OD都在坐标轴的正半轴上，OD＝3，另两边与反比例函数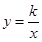
(k≠0)的图象分别相交于点E、F，且DE＝2．过点E作EH⊥x轴于点H，过点F作FG⊥EH于点G．回答下面的问题：
(1)①求反比例函数的解析式．
②当四边形AEGF为正方形时，求点F的坐标．
(2)小亮进一步研究四边形AEGF的特征后提出问题：“当AE＞EG时，矩形AEGF与矩形DOHE能否全等？能否相似？”
针对小亮提出的问题，请你判断这两个矩形能否全等(直接写出结论即可)．这两个矩形能否相似？若能相似，求出相似比；若不能相似，试说明理由．
如图，在△ABC中，D是BC边上的点(不与点B，C重合)，连接AD．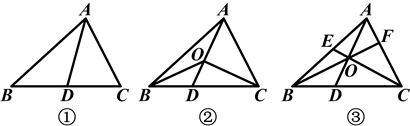
问题引入：
(1)如图①，当点D是BC边上的中点时，S△ABD︰S△ABC＝________；当点D是BC边上任意一点时，S△ABD︰S△ABC＝________(用图中已有线段表示)．
探索研究：
(2)如图②，在△ABC中，O点是线段AD上的一点(不与点A，D重合)，连接BO，CO，试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比，并说明理由．
拓展应用：
(3)如图③，O是线段AD上一点(不与点A，D重合)，连接BO并延长交AC于点F，连接CO并延长交AB于点E，试猜想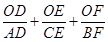
的值，并说明理由．