一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量(件与售价(元件)为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
(元件) |
4 |
5 |
6 |
(件 |
10000 |
9500 |
9000 |
(1)求与的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于15元件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(3)抗疫期间,该商场这种商品售价不大于15元件时,每销售一件商品便向某慈善机构捐赠元,捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出的取值范围.
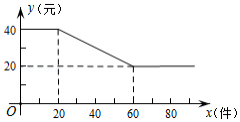
某工厂生产一种火爆的网红电子产品,每件产品成本16元、工厂将该产品进行网络批发,批发单价 (元 与一次性批发量 (件 为正整数)之间满足如图所示的函数关系.
(1)直接写出 与 之间所满足的函数关系式,并写出自变量 的取值范围;
(2)若一次性批发量不超过60件,当批发量为多少件时,工厂获利最大?最大利润是多少?
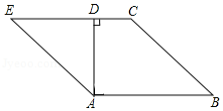
小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 ,箱长 ,拉杆 的长度都相等,即 , , 在 上, 在 上,支杆 , , , ,请根据以上信息,解决下列问题.
(1)求 的长度(结果保留根号);
(2)求拉杆端点 到水平滑杆 的距离(结果保留根号).

如图,在四边形 中, , , ,延长 到点 ,使 ,连接 .
(1)求证: ;
(2)若 , ,求四边形 的面积.
某中学为了提高学生的综合素质,成立了以下社团: .机器人, .围棋, .羽毛球, .电影配音.每人只能加入一个社团.为了解学生参加社团的情况,从参加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下两幅不完整的统计图,其中图(1)中 所占扇形的圆心角为 .
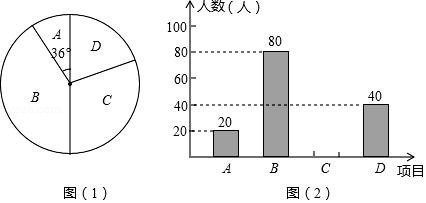
根据以上信息,解答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图补充完整;
(3)若该校共有1000名学生加入了社团,请你估计这1000名学生中有多少人参加了羽毛球社团;
(4)在机器人社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加机器人大赛.用树状图或列表法求恰好选中甲、乙两位同学的概率.
在 中, , 是 内一点,连接 , ,在 左侧作 ,使 ,以 和 为邻边作 ,连接 , .
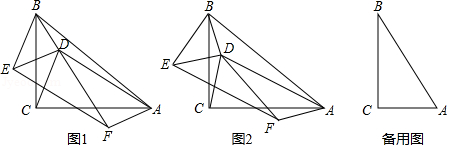
(1)若 , .
①如图1,当 , , 三点共线时, 与 之间的数量关系为 .
②如图2,当 , , 三点不共线时,①中的结论是否仍然成立?请说明理由.
(2)若 , , ,且 , , 三点共线,求 的值.