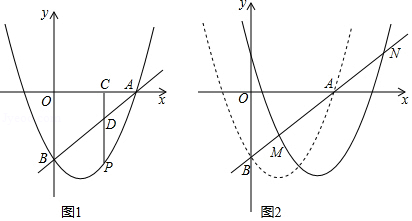
如图,抛物线 与 轴正半轴交于点 ,与 轴交于点 .
(1)求直线 的解析式及抛物线顶点坐标;
(2)如图1,点 为第四象限且在对称轴右侧抛物线上一动点,过点 作 轴,垂足为 , 交 于点 ,求 的最大值,并求出此时点 的坐标;
(3)如图2,将抛物线 向右平移得到抛物线 ,直线 与抛物线 交于 , 两点,若点 是线段 的中点,求抛物线 的解析式.
丹东市某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
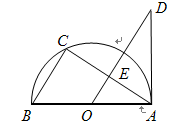
如图,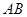 为半圆
为半圆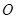 的直径,点C在半圆
的直径,点C在半圆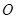 上,过点
上,过点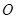 作
作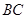 的平行线交
的平行线交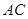 于点
于点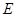 ,交过点
,交过点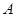 的直线于点
的直线于点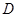 ,且
,且 .
.
(1)求证: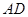 是半圆O的切线;
是半圆O的切线;
(2)若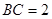 ,AC=2
,AC=2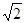 ,求
,求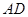 的长
的长
如图,已知反比例函数 的图象经过点(
的图象经过点( ,8),直线
,8),直线 经过该反比例函数图象上的点Q(4,
经过该反比例函数图象上的点Q(4, ).
).
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与 轴、
轴、 轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
某联欢会上有一个有奖游戏,规则如下:有5张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,其余3张是哭脸.现将5张纸牌洗匀后背面朝上摆放到桌上,若翻到的纸牌中有笑脸就有奖,没有笑脸就没有奖.
(1)小芳获得一次翻牌机会,她从中随机翻开一张纸牌.小芳得奖的概率是 .
(2)小明获得两次翻牌机会,他同时翻开两张纸牌.小明认为这样得奖的概率是小芳的两倍,你赞同他的观点吗?请用树形图或列表法进行分析说明.(用 、
、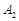 分别代表两张笑脸,
分别代表两张笑脸, 、
、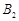 、
、 分别代表三张哭脸)
分别代表三张哭脸)
如图,某风景区的湖心岛有一凉亭A,其正东方向有一棵大树B,小明想测量A、B之间的距离,他从湖边的C处测得A在北偏西45°方向上,测得B在北偏东32°方向上,且量得B、C之间的距离为100米,根据上述测量结果,请你帮小明计算A、B之间的距离是多少?(结果精确到1米。参考数据:sin32°=0.5299,cos32°=0.8480)