"通过等价变换，化陌生为熟悉，化未知为已知"是数学学习中解决问题的基本思维方式，例如：解方程 ，就可以利用该思维方式，设 ，将原方程转化为： 这个熟悉的关于 的一元二次方程，解出 ，再求 ，这种方法又叫"换元法"．请你用这种思维方式和换元法解决下面的问题．
已知实数 ， 满足 ，求 的值．
如图，一次函数y=ax+b的图象与反比例函数y=
的图象交于M、N两点．
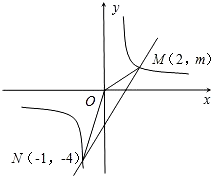
求：（1）反比例函数与一次函数的解析式；
（2）根据图象写出反比例函数的值＞一次函数的值的x的取值范围．
正方形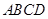
边长为4，
、
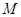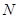分别是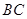
、
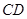上的两个动点，当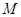点在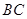上运动时，保持
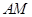和
垂直，设MB=x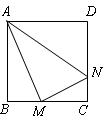
（1）证明：
；
（2）当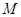点运动到什么位置时
，
求此时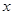
的值．
烟花广告公司将一块广告牌任务交给师徒两人，已知师傅单独完成时间是徒弟单独完成时间的
，现由徒弟先做1天，师徒再合作2天完成。
⑴师徒两人单独完成任务各需要几天？
⑵若完成后得到报酬720元，你若是部门经理，按各人完成的工作量计算报酬，该如何分配？
如图，
在方格纸中
（1）请在方格纸上建立平面直角坐标系，使
，并求出
点坐标；
（2）以原点
为位似中心，相似比为2，在第一象限内将放大，画出放大后的图形
；
（3）计算的面积
．
若关于x的分式方程
－
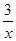=1无解，求m的值。