如图1，抛物线y＝ax²+b的顶点坐标为（0，﹣1），且经过点A（﹣2，0）．

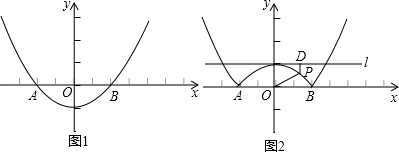
（1）求抛物线的解析式；

（2）若将抛物线y＝ax²+b中在x轴下方的图象沿x轴翻折到x轴上方，x轴上方的图象保持不变，就得到了函数y＝|ax²+b|图象上的任意一点P，直线l是经过（0，1）且平行与x轴的直线，过点P作直线l的垂线，垂足为D，猜想并探究：PO与PD的差是否为定值？如果是，请求出此定值；如果不是，请说明理由．

（注：在解题过程中，如果你觉得有困难，可以阅读下面的材料）

附阅读材料：

1．在平面直角坐标系中，若A、B两点的坐标分别为A（x₁，y₁），B（x₂，y₂），则A，B两点间的距离为 $\left|\mathit{AB}\right|=\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2}$，这个公式叫两点间距离公式．

例如：已知A，B两点的坐标分别为（﹣1，2），（2，﹣2），则A，B两点间的距离为 $\left|\mathit{AB}\right|=\sqrt{{(-1-2)}^2+{(2+2)}^2}=5$．

2．因式分解：x⁴+2x²y²+y⁴＝（x²+y²）²．

科目 数学   题型 解答题   难度 较难

知识点： 二次函数图象与几何变换 待定系数法求二次函数解析式 二次函数综合题