(·湖州市 第22题 10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
(·衢州市 第23题 6分)高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,乐乐和颖颖相约到杭州市的某游乐园游玩,乐乐乘私家车从衢州出发1小时后,颖颖乘坐高铁从衢州出发,先到杭州火车站,然后再转车出租车取游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示.
请结合图象解决下面问题:
(1)高铁的平均速度是每小时多少千米?
(2)当颖颖达到杭州火车东站时,乐乐距离游乐园还有多少千米?
(3)若乐乐要提前18分钟到达游乐园,问私家车的速度必须达到多少千米/小时?
(·温州卷 第20题 8分)各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形。如何计算它的面积?奥地利数学家皮克(G.Pick,1859~1942)证明了格点多边形的面积公式: ,其中
,其中 表示多边形内部的格点数,
表示多边形内部的格点数, 表示多边形边界上的格点数,S表示多边形的面积。如图,
表示多边形边界上的格点数,S表示多边形的面积。如图, ,
,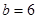 ,
, 。
。
(1)请在图甲中画一个格点正方形,使它内部只含有4个格点,并写出它的面积;
(2)请在图乙中画一个格点三角形,使它的面积为 ,且每条边上除顶点外无其它格点。(注:图甲、图乙在答题纸上)
,且每条边上除顶点外无其它格点。(注:图甲、图乙在答题纸上)
(·绍兴市 第21题 10分)如果抛物线 过定点M(1,1),则称此抛物线为定点抛物线。
过定点M(1,1),则称此抛物线为定点抛物线。
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的一个解析式。小敏写出了一个答案: ,请你写出一个不同于小敏的答案;
,请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线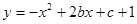 ,求该抛物线顶点纵坐标的值最小时的解析式,请你解答。
,求该抛物线顶点纵坐标的值最小时的解析式,请你解答。
(·嘉兴市 第24题 14分)类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)概念理解
如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)问题探究
①小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由。
②如图2,小红画了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将Rt△ABC沿∠ABC的平分线BB'方向平移得到△A'B'C',连结AA',BC'.小红要是平移后的四边形ABC'A'是“等邻边四边形”,应平移多少距离(即线段BB'的长)?
(3)应用拓展
如图3,“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD==90°,AC,BD为对角线,AC= AB.试探究BC,CD,BD的数量关系.
AB.试探究BC,CD,BD的数量关系.