如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的 .
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.

如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4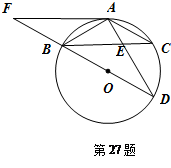
求证:△ABE∽△ADB;
求AB的长
延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
2011年3月11日13时46分日本发生了9.0级大地震,伴随着就是海啸。山坡上有一棵与水平面垂直的大树,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4米。求∠DAC的度数;
求这棵大树原来的高度是多少米?(结果精确到个位,参考数据:
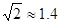 ,
,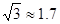 ,
,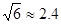 )
)
西北地区冬季干旱,平安社区每天需从外地调运饮用水120吨.有关部门紧急部署,从甲、乙两水厂调运饮用水到供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨.从两水厂运水到平安社区供水点的路程和运费如下表:
| 到平安社区供水点的路程(千米) |
运费(元/吨·千米) |
|
| 甲厂 |
20 |
12 |
| 乙厂 |
14 |
15 |
若某天调运水的总运费为26700元,则从甲、乙两水厂各调运了多少吨饮用水?
设从甲厂调运饮用水x吨,总运费为W元,试写出W关于与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?
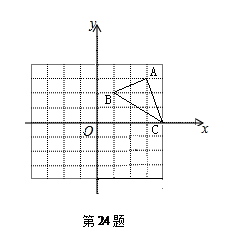
如图所示,每一个小方格都是边长为1的单位正方形。△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系。画出△ABC先向左平移5个单位,再向上平移1个单位的△A1B1C1,并写出点B1的坐标;
画出将△ABC绕点O顺时针旋转90°后的△A2B2C2,并求出点A旋转到A2所经过的路径长。
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连结BF。BD与CD有什么数量关系,并说明理由;
当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由。
