如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D, ,求 的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.

解方程组: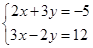
【问题提出】如图1,四边形ABCD中,AD=CD,∠ABC=120°,∠ADC=60°,AB=2,BC=1,求四边形ABCD的面积.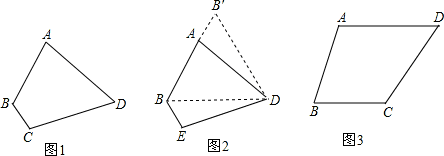
【尝试解决】
旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.
(1)如图2,连接 BD,由于AD=CD,所以可将△DCB绕点D顺时针方向旋转60°,得到△DAB′,则△BDB′的形状是.
(2)在(1)的基础上,求四边形ABCD的面积.
[类比应用]如图3,四边形ABCD中,AD=CD,∠ABC=75°,∠ADC=60°,AB=2,BC=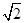 ,求四边形ABCD的面积.
,求四边形ABCD的面积.
在初中数学中,我们学习了“两点间的距离”、“点到直线的距离”、“平行线之间的距离”,距离的本质是“最短”,图形之间的距离总可以转化为两点之间的距离,如“垂线段最短”的性质,把点到直线的距离转化为点到点(垂足)的距离.
一般的,一个图形上的任意点A与另一个图形上的任意点B之间的距离的最小值叫做两个图形的距离.
(1)如图1,过A,B分别作垂线段AC、AD、BE、BF,则线段AB和直线l的距离为垂线段的长度.
(2)如图2,Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB,AD=2,那么线段AD与线段BC的距离为.
(3)如图3,若长为1cm的线段CD与已知线段AB的距离为1.5cm,请用适当的方法表示满足条件的所有线段CD.
注:若满足条件的线段是有限的,请画出;若满足条件的线段是无限的,请用阴影表示其所在区域.(保留画图痕迹)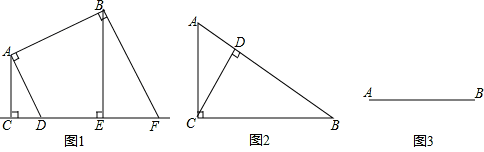
甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发2分钟,且到达乙地后在原地等待货车,则当x=小时,货车和轿车相距30千米.
如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为3,AE=5,求∠DAE的正弦值.