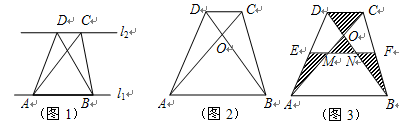
“一号龙卷风”给小岛O造成了较大的破坏,救灾部门迅速组织力量,从仓储D处调集救援物资,计划先用汽车运到与D在同一直线上的C、B、A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°,CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,问这批物资在哪个码头装船,最早运抵小岛O?(在物资搬运能力上每个码头工作效率相同,参考数据: ).

已知一次函数 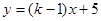 的图象经过点
的图象经过点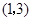 .
.
(1)求出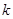 的值;
的值;
(2)求当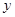 =1时,
=1时,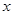 的值.
的值.
解方程: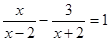 .
.
计算: .
.
在平面坐标系xoy中,直线 与x,y轴交于点A,B,作△AOB为外接⊙E.将直角三角板的30°角的顶点C摆放在圆弧上,三角板的两边始终过点O,A,并且不断地转动三角板.
与x,y轴交于点A,B,作△AOB为外接⊙E.将直角三角板的30°角的顶点C摆放在圆弧上,三角板的两边始终过点O,A,并且不断地转动三角板.
(1)如图1,当点C与B重合时,连接OE求扇形EOA的面积;
(2)当 时,求经过A,O,C三点的抛物线的解析式,直接写出顶点坐标;
时,求经过A,O,C三点的抛物线的解析式,直接写出顶点坐标;
(3)如图2,在转动中,过C作⊙E的切线,交y轴于D,当A,C,D,B四点围成的四边形是梯形时,求点D的坐标.
阅读材料:如图1:直线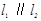 ,点A,B,C,D分别在
,点A,B,C,D分别在 和
和 上,因为“两平行线间的距离处处相等”,所以
上,因为“两平行线间的距离处处相等”,所以 ,
, .
.
解决问题:如图2:在梯形ABCD中,AB∥CD,AC,BD相交于点O, (n>1的正实数),梯形ABCD的面积为S.请回答下列问题:
(n>1的正实数),梯形ABCD的面积为S.请回答下列问题:
(1)请直接写出相应的值:①当n=2时, =▲S;②当n=3时,
=▲S;②当n=3时, =▲S;
=▲S;
③ =▲S(用n的代数式表示);
=▲S(用n的代数式表示);
(2)如图3,点E,F分别在AD,BC的中点, EF分别交AC,BD于M,N,,求 的值(用n的代数式表示);
的值(用n的代数式表示);
(3)在(2)中,根据上面的结论,当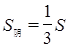 时,直接写出n的值.
时,直接写出n的值.