阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有： ， ， ， ．
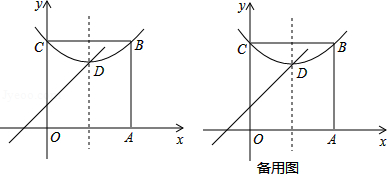
问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线 经过B、C两点，顶点D在正方形内部．
（1）直接写出点D（m，n）所有的特征线；
（2）若点D有一条特征线是y＝x+1，求此抛物线的解析式；
（3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于坐标轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？
（1）计算：
；
（2）解不等式：
＜1．
（本小题14分）如图，二次函数y=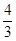
x2+bx+c的图象与x轴交于A（3，0），B（﹣1，0），与y轴交于点C．若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC边运动，其中一点到达端点时，另一点也随之停止运动．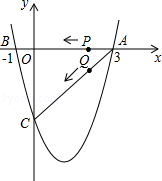
（1）求该二次函数的解析式及点C的坐标；
（2）当点P运动到B点时，点Q停止运动，这时，在x轴上是否存在点E，使得以A，E，Q为顶点的三角形为等腰三角形？若存在，请求出E点坐标；若不存在，请说明理由．
（3）当P，Q运动到t秒时，△APQ沿PQ翻折，点A恰好落在抛物线上D点处，请判定此时四边形APDQ的形状，并求出D点坐标．
（4）在AC段的抛物线上有一点R到直线AC的距离最大，请直接写出点R的坐标．
（本小题10分）为喜迎“端午”佳节，黄冈南湖食品工业园某食品公司推出一种新礼盒，每盒成本20元，在“端午”节前20天进行销售后发现，该礼盒在这20天内的日销售量p（盒）与时间x（天）的关系如下表：
| 时间x（天） |
第1天 |
第2天 |
第3天 |
第4天 |
第5天 |
第…天 |
| 日销售量p（盒） |
78 |
76 |
74 |
72 |
70 |
…… |
在这20天内，前10天每天的销售价格y1（元/盒）与时间x（天）的函数关系式为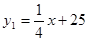
（1≤x≤10，且x为整数），后10天每天的销售价格y2（元/盒）与时间x（天）的函数关系式为
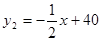（11≤x≤20，且x为整数），
（1）直接写出日销售量p（盒）与时间x（天）之间的函数关系式；
（2）请求出这20天中哪天的日销售利润最大？最大日销售利润是多少？
（3）“端午”当天，销售价格（元/盒）比第20天的销售价格降低a元（a>0），而日销售量比第20天提高了a盒，日销售额比前20天中的最大日销售利润多284元，求a的值．（注：销售利润=（售价—成本价）×销售量）
（本小题7分）图①、②分别是某种型号跑步机的实物图与示意图，已知踏板CD长为1．6m，CD与地面DE的夹角∠CDE为12°，支架AC长为0．8m，∠ACD为80°，求跑步机手柄的一端A的高度h（精确到0．1m）．
（参考数据：sin12°=cos78°≈0．21，sin68°=cos22°≈0．93，tan68°≈2．48）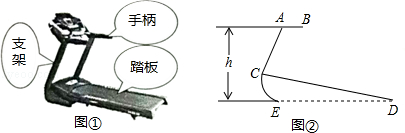
（本小题8分）如图，⊙O的直径AB垂直于弦CD，垂足为点E，过点C作⊙O 的切线，交AB的延长线于点P，联结PD．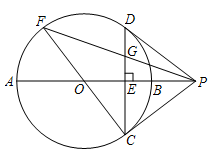
（1）判断直线PD与⊙O的位置关系，并加以证明；
（2）连接CO并延长交⊙O于点F，联结FP交CD于点G，如果CF=10，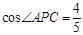
，求EG的长．