当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量 y(本)与销售单价 x(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠 a(0< a≤6)元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求 a的值.
图(1)是正方体木块,把它切去一块,可能得到形如图(2)、(3)、(4)、(5)的木块。
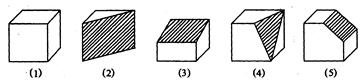
我们知道,图(1)的正方体木块有8个顶点,12条棱,6个面,请你将图(2),(3),(4),(5)中木块的顶点数,棱数,面数填入下表:
| 图 |
顶点数 |
棱数 |
面数 |
| (1) |
8 |
12 |
6 |
| (2) |
|||
| (3) |
|||
| (4) |
|||
| (5) |
观察上表,请你归纳上述各种木块的顶点数,棱数,面数之间的数量关系,这种数量关系是:_______________
在
 中,
中,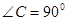 ,
, 的正弦、余弦之间有什么关系?请给出证明过程。
的正弦、余弦之间有什么关系?请给出证明过程。已知锐角
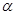 满足:
满足: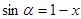 ,
,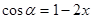 ,求
,求 的值。
的值。
数学课上,李老师出示了如下框中的题目.小敏与同桌小聪讨论后,进行了如下解答:
特殊情况,探索结论.当点
 为
为 的中点时,确定线段
的中点时,确定线段 与
与 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:
 (填“>”,“<”或“=”).
(填“>”,“<”或“=”).
特例启发,解答题目
解:题目中, 与
与 的大小关系是:
的大小关系是:
 (填“>”,“<”或“=”).理由如下:
(填“>”,“<”或“=”).理由如下:
如图1,过点 作
作 ,交
,交 于点
于点 .(请你完成以下解答过程)
.(请你完成以下解答过程)拓展结论,设计新题
在等边三角形 中,点
中,点 在直线
在直线 上,点
上,点 在直线
在直线 上,且
上,且 .若
.若 的边长为1,
的边长为1, ,则
,则 的长为 (请你画出图形并直接写出结果,图没画或画错均不得分).
的长为 (请你画出图形并直接写出结果,图没画或画错均不得分).
已知:如图,锐角△ABC的两条高CD、BE相交于点O,且OB=OC
求证:△ABC是等腰三角形
连结AO,判断AO与BC的位置关系,并说明理由.
如图,点E,F在BC上,BE=CF,∠A=∠D ,∠B=∠C.求证:△ABF≌△DCE.