已知,如图,抛物线 y= ax 2+ bx+ c( a≠0)的顶点为 M(1,9),经过抛物线上的两点 A(﹣3,﹣7)和 B(3, m)的直线交抛物线的对称轴于点 C.
(1)求抛物线的解析式和直线 AB的解析式.
(2)在抛物线上 A、 M两点之间的部分(不包含 A、 M两点),是否存在点 D,使得 S △ DAC=2 S △ DCM?若存在,求出点 D的坐标;若不存在,请说明理由.
(3)若点 P在抛物线上,点 Q在 x轴上,当以点 A, M, P, Q为顶点的四边形是平行四边形时,直接写出满足条件的点 P的坐标.

如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF,求证:△DEF为等边三角形.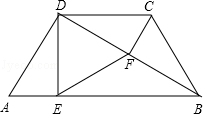
如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.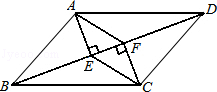
(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形.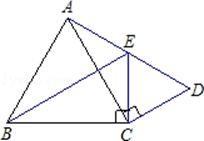
已知AD⊥BC,BE=CE,∠ABC=2∠C,BF为∠B的平分线.求证:AB=2DE.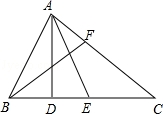
如图,在△ABC中,AB=AC,AD平分∠BAC.求证:∠DBC=∠DCB.