某书店在"读书节"之前,图书按标价销售,在"读书节"期间制定了活动计划.
(1)"读书节"之前小明发现:购买5本 A图书和8本 B图书共花279元,购买10本 A图书比购买6本 B图书多花162元,请求出 A、 B图书的标价;
(2)"读书节"期间书店计划用不超过3680元购进 A、 B图书共200本,且 A图书不少于50本, A、 B两种图书进价分别为24元、16元;销售时准备 A图书每本降价1.5元, B图书价格不变,那么书店如何进货才能使利润最大?
《中学生体质健康标准》规定学生体质健康等级标准为:86分及以上为优秀;76分~85分为良好;60分~75分为及格;59分及以下为不及格.某校抽取八年级学生人数的10%进行体质测试,测试结果如图.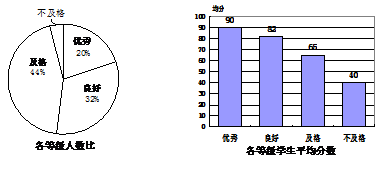
(1)在抽取的学生中不及格人数所占的百分比是;
(2)小明按以下方法计算出所抽取学生测试结果的平均分是:(90+82+65+40)÷4=69.25.根据所学的统计知识判断小明的计算是否正确,若不正确,请写出正确的算式并计算出结果.
如图,在梯形ABCD中 AB‖DC,DB平分∠ADC,过点A作AE‖BD,交CD的延长线于点E,且∠C=2∠E
求证:梯形ABCD是等腰梯形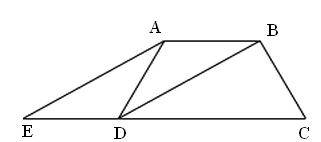
如图,若抛物线Y=X2改为抛物线Y= X2+BX+C其他条件不变求矩形ABCD的面积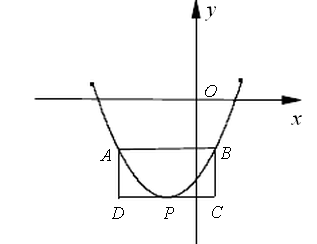
如图,一块长方形铁皮的长是宽的2倍,四个角各截去一个正方形,制成高是5CM,容积是500CM3的无盖长方体容器,求这块铁皮的长和宽
小峰骑自行车去小宝家聚会,一路上小峰注意到,每隔9分钟就有一辆公交车从后方超越小峰,小峰骑车到半路,车坏了,小峰只好打的去小宝家,这时小峰又发现出租车也是每隔9分钟超越一辆公交车,已知出租车的速度是小峰骑车速度的5倍,那么如果公交车的发车时间间隔和行驶速度固定的话,公交车的发车时间间隔为多少分钟?