△ABC和△DEF是两个全等的等腰直角三角形, ,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且 时,求证: ;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当 , 时BC的长.

如图①,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF=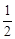 AB,
AB,
(1)求证:△ABE≌△ADF.
(2)阅读下列材料:如图②,把△ABC沿直线平移线段BC的长度,可以变到△ECD的位置;如图③,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;如图④,以点A为中心,把△ABC旋转180°,可以变到△AED的位置,像这样其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
图①图②图③图④
请回答下列问题:
(1)在图①中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置?
(2)指出图①中线段BE与DF之间的关系.
怎样将下图中的甲图变成乙图?
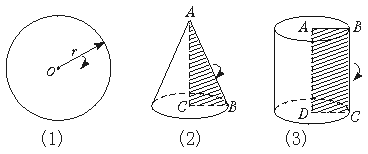
下列三幅图案分别是由什么“基本图形”经过平移或旋转而得到的?
1.
2.
3.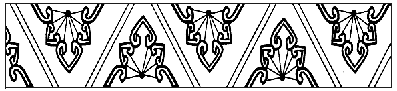
请观察图,图中是否存在这样的两个三角形,其中一个是另一个旋转得到的?
观察下列图形,它可以看作是什么“基本图形”通过怎样的旋转而得到的?