如图①,在△ABC中, , , ,D为AB的中点,EF为△ACD的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).
(1)计算矩形EFGH的面积;
(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为 时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1,将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2,设旋转角为α,求cosα的值.

如图:在平面直角坐标系中,将长方形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB=3,AD=6,将纸片沿过点M的直线折叠(点M在边AB上),使点B落在边AD上的E处(若折痕MN与x轴相交时,其交点即为N),过点E作EQ⊥BC于Q,交折痕于点P。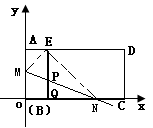
(1)①当点 分别与AB的中点、A点重合时,那么对应的点P分别是点
分别与AB的中点、A点重合时,那么对应的点P分别是点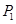 、
、 ,则
,则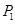 (,)、
(,)、 (,);②当∠OMN=60°时,对应的点P是点
(,);②当∠OMN=60°时,对应的点P是点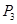 ,求
,求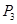 的坐标;
的坐标;
(2)若抛物线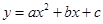 ,是经过(1)中的点
,是经过(1)中的点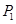 、
、 、
、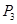 ,试求a、b、c的值;
,试求a、b、c的值;
(3)在一般情况下,设P点坐标是(x,y),那么y与x之间函数关系式还会与(2)中函数关系相同吗(不考虑x的取值范围)?请你利用有关几何性质(即不再用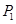 、
、 、
、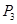 三点)求出y与x之间的关系来给予说明.
三点)求出y与x之间的关系来给予说明.
(1)观察发现如题(a)图,若点A,B在直线 同侧,在直线
同侧,在直线 上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线
上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线 的对称点
的对称点 ,连接
,连接 ,与直线
,与直线 的交点就是所求的点P 再如题(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小. 做法如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为.
的交点就是所求的点P 再如题(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小. 做法如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为.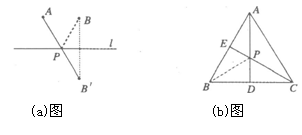
(2)实践运用
如题(c)图,已知⊙O的直径CD为4,弧AD所对圆心角的度数为60°,点B是弧AD的中点,请你在直径CD上找一点P,使BP+AP的值最小,并求BP+AP的最小值.
(3)拓展延伸
如题(d)图,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.保留
作图痕迹,不必写出作法.
如图,BD是⊙O的直径,A、C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.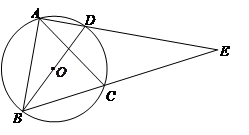
(1)求证:△ABD∽△AEB;
(2)若AD=1,DE=3,求⊙O半径的长.
一量角器所在圆的直径为10厘米,其外缘有A、B两点,其读数、分别为71°和47°.
(1).劣弧AB所对圆心角是多少度?
(2).求劣弧AB的长;
(3)问A、B之间的距离是多少?(可用计算器,精确到0.1)
已知双曲线 和直线AB的图象交于点A(-3,4),AC⊥x轴于点C.
和直线AB的图象交于点A(-3,4),AC⊥x轴于点C.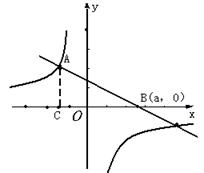
(1)求双曲线 的解析式;
的解析式;
(2)当直线AB绕着点A转动时,与x轴的交点为B(a,0),并与双曲线 另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式.,并指出a的取值范围.
另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式.,并指出a的取值范围.