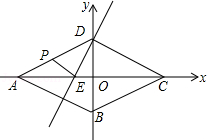
如图,以菱形 对角线交点为坐标原点,建立平面直角坐标系, 、 两点的坐标分别为 , 、 ,直线 交 于 ,动点 从点 出发,以每秒2个单位的速度沿着 的路线向终点 匀速运动,设 的面积为 ,点 的运动时间为 秒.
(1)求直线 的解析式;
(2)求 与 之间的函数关系式,并写出自变量 的取值范围;
(3)当 为何值时, ?并求出此时直线 与直线 所夹锐角的正切值.
已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.
求证:(1)BD=AE.
(2)若线段AD=5,AB=17,求线段ED的长。
如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B.试说明AD+AB=BE.
如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A(-1,5),B(-1,0),C(-4,3).
(1)画出△ABC关于y轴对称的△A1B1C1;(其中A1、B1、C1是A、B、C的对应点,不写画法)
(2)写出A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.
计算:如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD.求证:AC=DF.
如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B.试说明AD+AB=BE.