学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.
学生借阅图书的次数统计表
借阅图书的次数 |
0次 |
1次 |
2次 |
3次 |
4次及以上 |
人数 |
7 |
13 |
|
10 |
3 |
请你根据统计图表中的信息,解答下列问题:
(1) , .
(2)该调查统计数据的中位数是 ,众数是 .
(3)请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.

下列命题的题设是什么?结论是什么?
(1)对顶角相等;(2)两条直线相交,只有一个交点;(3)如果a2=b2,那么a=b.
请将下列命题改写成“如果……那么……”的形式:
(1)等角的余角相等;
(2)垂直于同一条直线的两直线平行;
(3)平行线的同旁内角的平分线互相垂直.
如图,平移△ABC,使得△ABC的边AB移到DE的位置.下面是小明的作业,他的做法完全正确,可由于不小心将一团墨汁沾染了作业本,如图,请你设法帮小明补全平移前后的△ABC和△DEF.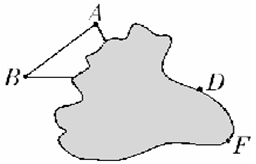
如图,经过平移,△ABC的边AB移到了EF,作出平移后的三角形.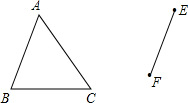
如图,△DEF是△ABC经过平移得到的。
(1)请指出平移的方向,量出平移的距离;
(2)如果点M、N是边AB、DE的中点,那么点M和点N的距离是多少?线段CM和FN相等吗?