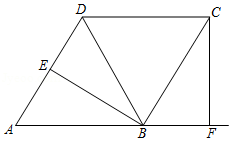
如图,菱形 中,作 、 ,分别交 、 的延长线于点 、 .
(1)求证: ;
(2)若点 恰好是 的中点, ,求 的值.
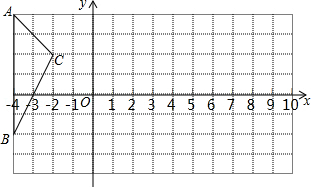
如图,已知抛物线 的图象经过点 , ,与 轴交于点 ,抛物线的顶点为 ,对称轴与 轴相交于点 ,连接 .
(1)求抛物线的解析式.
(2)若点 在直线 上,当 时,求点 的坐标.
(3)在(2)的条件下,作 轴于 ,点 为 轴上一动点, 为直线 上一动点, 为抛物线上一动点,当以点 , , , 四点为顶点的四边形为正方形时,求点 的坐标.

如图, 是 的直径,点 , 在 上, ,点 在 的延长线上, .
(1)求证: 是 的切线;
(2)若 , ,求 的半径长.

校园超市以4元 件购进某物品,为制定该物品合理的销售价格,对该物品进行试销调查.发现每天调整不同的销售价,其销售总金额为定值,其中某天该物品的售价为6元 件时,销售量为50件.
(1)设售价为 元 件时,销售量为 件.请写出 与 的函数关系式;
(2)若超市考虑学生的消费实际,计划将该物品每天的销售利润定为60元,则该物品的售价应定为多少元 件?
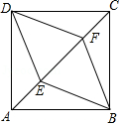
如图, , 是正方形 的对角线 上的两点,且 .
(1)求证:四边形 是菱形;
(2)若正方形边长为4, ,求菱形 的面积.
如图, 中, , , .
(1)请画出将 向右平移8个单位长度后的△ ;
(2)求出 的余弦值;
(3)以 为位似中心,将△ 缩小为原来的 ,得到△ ,请在 轴右侧画出△ .