(2) , ,
,
;
又 ,
,
;
方法一:在 中, ,
连接 ,设 的半径为 ,则在 中, ,即
解得:
方法二: ,过点 作 于点 ,则
在 中,
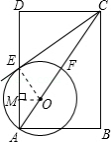
本题考查了圆的综合题:圆的切线垂直于过切点的半径;利用勾股定理计算线段的长.
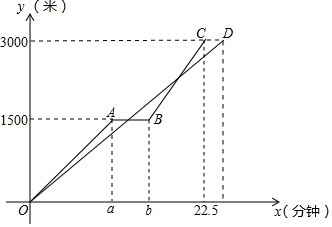
“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米 分的速度骑行一段时间,休息了5分钟,再以 米 分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程 (米 与时间 (分钟)的关系如图,请结合图象,解答下列问题:
(1) , , ;
(2)若小军的速度是120米 分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是 米 分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出 的取值范围.
为养成学生课外阅读的习惯,各学校普遍开展了“我的梦 中国梦”课外阅读活动.某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:
(1)表中 , ;
(2)请补全频数分布直方图中空缺的部分;
(3)样本中,学生日阅读所用时间的中位数落在第 组;
(4)请估计该校七年级学生日阅读量不足1小时的人数.
|
组别 |
时间段(小时) |
频数 |
频率 |
|
1 |
|
10 |
0.05 |
|
2 |
|
20 |
0.10 |
|
3 |
|
80 |
|
|
4 |
|
|
0.35 |
|
5 |
|
12 |
0.06 |
|
6 |
|
8 |
0.04 |

如图,在 中, 于 , , , , 分别是 , 的中点.
(1)求证: , ;
(2)连接 ,若 ,求 的长.

如图,已知抛物线 与 轴交于点 和点 ,与 轴交于点 ,连接 交抛物线的对称轴于点 , 是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点 和点 的坐标;
(3)若点 在第一象限内的抛物线上,且 ,求 点坐标.
注:二次函数 的顶点坐标为 ,

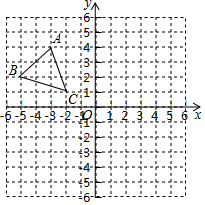
如图,平面直角坐标系内,小正方形网格的边长为1个单位长度, 的三个顶点的坐标分别为 , , .
(1)画出 关于 轴的对称图形△ ;
(2)画出将 绕原点 逆时针方向旋转 得到的△ ;
(3)求(2)中线段 扫过的图形面积.