都匀某校准备组织学生及家长代表到桂林进行社会实践活动,为便于管理,所有人员必须乘坐同一列高铁,高铁单程票价格如表所示,二等座学生票可打7.5折,已知所有人员都买一等座单程火车票需6175元,都买二等座单程火车票需3150元;如果家长代表与教师的人数之比为 .
运行区间 |
票价 |
||
起点站 |
终点站 |
一等座 |
二等座 |
都匀 |
桂林 |
95(元 |
60(元 |
(1)参加社会实践活动的老师、家长代表与学生各有多少人?
(2)由于各种原因,二等座单程火车票只能买 张 参加社会实践的总人数),其余的须买一等座单程火车票,在保证所有人员都有座位的前提下,请你设计最经济的购票方案,并写出购买单程火车票的总费用 与 之间的函数关系式.
(3)在(2)的方案下,请求出当 时,购买单程火车票的总费用.
如图,直线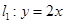 与直线
与直线 在同一平面直角坐标系内交于点P,且直线
在同一平面直角坐标系内交于点P,且直线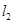 与x轴交于点A. 求直线
与x轴交于点A. 求直线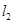 的解析式及△OAP的面积.
的解析式及△OAP的面积.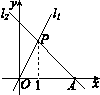
已知:如图,AC=AD,AB是∠CAD的角平分线.求证:BC=BD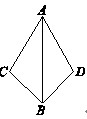
如图,已知二次函数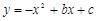 的图象经过A(
的图象经过A(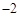 ,
,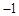 ),B(0,7)两点.
),B(0,7)两点.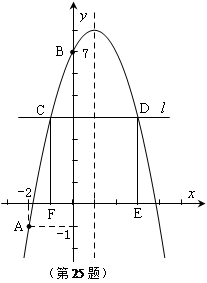
⑴求该抛物线的解析式及对称轴;
⑵当 为何值时,
为何值时,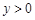 ?
?
⑶在 轴上方作平行于
轴上方作平行于 轴的直线
轴的直线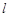 ,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作
,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作 轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.
轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.
如图,Rt△ABO的顶点A是双曲线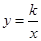 与直线
与直线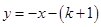 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥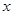 轴于B且S△ABO=
轴于B且S△ABO=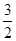 .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标和△AOC的面积。
某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,为了使5月份的营业额达到633.6万元,那么3月份到5月份的平均增长率为多少?