求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法 更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.
例如:求91与56的最大公约数
解:
请用以上方法解决下列问题:
(1)求108与45的最大公约数;
(2)求三个数78、104、143的最大公约数.

如图所示,∠MBN=45°,若△ABC的顶点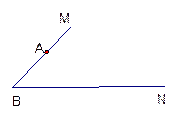
A在射线BM上,且AB= ,点C在射线BN运动(C
,点C在射线BN运动(C
不与B重合).请你探究:
(1)当BC=时,△ABC是直角三角形,并标出所有符合要求的C点;
(2)当BC的值在范围时,△ABC是锐角三角形;
(3)当BC的值在范围时,△ABC是钝角三角形 .
已知矩形ABCD,现将矩形沿对角线BD折叠,得到如图所示的图形,
(1)求证:△ABE≌△C’ DE
(2)若AB=6,AD=10,求S△ABE
求下列各式中的实数x.
(1)  ; (2)
; (2) 
( 10分)由于受金融危机的影响,某店经销的甲型号手机今年的售价比去年每台降价500元.如果卖出相同数量的手机,那么去年销售额为8万元,今年销售额只有6万元.
(1)今年甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划购进乙型号手机销售,已知甲型号手机每台进价为1000元,乙型号手机每台进价为800元,预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)若乙型号手机的售价为1400元,为了促销,公司决定每售出一台乙型号手机,返还顾客现金a元,而甲型号手机仍按今年的售价销售,要使(2)中所有方案获利相同,a应取何值?
某中学从2007年以来,一直坚持开展用眼健康方面的教育,并进行跟踪治疗. 为了调查全校学生的视力变化情况,从中抽取部分学生近几年视力检查的结果做了统计(如图1),并统计了2010年这部分学生的视力分布情况(如表1和图2).
 |
 |
||
 |
(1)根据以上图表中提供的信息写出:a=, b=, x+y=;
(2)由统计图中的信息可知,近几年学生视力为5.0的学生人数每年与上一年相比,增加最多的是年;若全校有3000名学生,请你估计2010年全校学生中视力达到5.0及5.0以上的约有人.