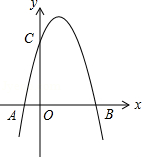
如图,二次函数 的图象与 轴的一个交点为 ,另一个交点为 ,且与 轴相交于 点.
(1)求 的值及 点坐标;
(2)在直线 上方的抛物线上是否存在一点 ,使得它与 , 两点构成的三角形面积最大,若存在,求出此时 点坐标;若不存在,请简要说明理由;
(3) 为抛物线上一点,它关于直线 的对称点为
①当四边形 为菱形时,求点 的坐标;
②点 的横坐标为 ,当 为何值时,四边形 的面积最大,请说明理由.
解方程组
计算:
(1)求 的值:
的值: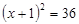 .
.
(2)计算: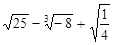 ;
;
【改编】某班同学在植树节这天参加了植树活动,已知男生比女生少4人,男生每人种3棵,女生每人种2棵,并且男女生所种树木棵数相同,设男生有x人,女生有y人,根据题意,列方程组正确的是()
A. |
B. |
C. |
D. |
【原创】(1)已知:如图1,BE⊥DE,∠1=∠B,∠2=∠D,试确定AB与CD的位置关系,并说明理由.
(2)若图形变化为如图2、图3所示,且满足∠1+∠2=90°,那么AB与CD还满足上述关系吗?若满足,选择一个图形进行证明.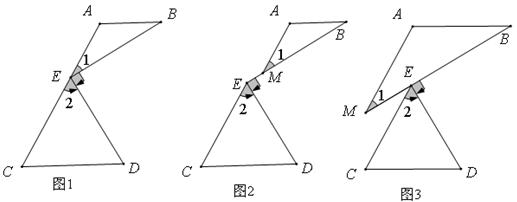
(本题7分)某中学新建了一栋四层的教学楼,每层楼有10间教室,进出这栋教学楼共有4个门,其中两个正门大小相同,两个侧门大小也相同.安全检查中,对4个门进行了测试,当同时开启一个正门和两个侧门时,2分钟内可以通过560名学生;当同时开启一个正门和一个侧门时,4分钟内可以通过800名学生.
(1)求平均每分钟开启一个正门和一个侧门各可以通过多少名学生?
(2)检查中发现,出现紧急情况时,因学生拥挤,出门的效率将降低20%,安全检查规定:在紧急情况下全楼的学生应在5分钟内通过这4个门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问:该教学楼建造的这4个门是否符合安全规定?请说明理由.