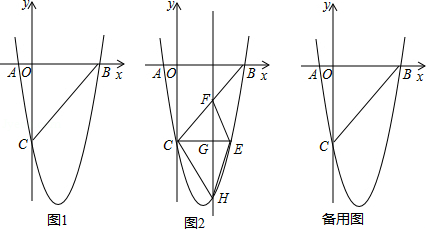
如图1，在平面直角坐标系中，已知抛物线 与 轴交于 ， 两点，与 轴交于点 ．
（1）求抛物线的函数表达式；
（2）若点 是 轴上的一点，且以 ， ， 为顶点的三角形与 相似，求点 的坐标；
（3）如图2， 轴与抛物线相交于点 ，点 是直线 下方抛物线上的动点，过点 且与 轴平行的直线与 ， 分别相交于点 ， ，试探究当点 运动到何处时，四边形 的面积最大，求点 的坐标及最大面积；
（4）若点 为抛物线的顶点，点 是该抛物线上的一点，在 轴， 轴上分别找点 ， ，使四边形 的周长最小，求出点 ， 的坐标．
如图，将三角形ABC绕点O旋转得到三角形A/B/C/，且∠AOB=300，∠AOB/=200，则
（1）点B的对应点是________________;
（2）线段OB的对应线段是____________;
（3）∠AOB的对应角是________________;
（4）三角形ABC旋转的角度是__________;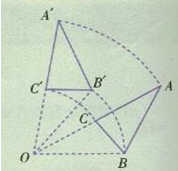
先化简再求值
,其中x=﹣1．（本题6分）
因式分解或解方程组（每小题5分，共10分）
（1）
（2）
如图，△ABC的边BC在直线
上，AC⊥BC，且AC＝BC，△EFP的边FP也在直线上，边EF与边AC重合，且EF＝FP。
（1）在图1中，请你通过观察、测量，猜想并写出AB与AP所满足的数量关系和位置关系；
（2）将△EFP沿直线向左平移到图2的位置时，EP交AC于点Q，连结AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系，请证明你的猜想。
如图①是一个长方形ABCD，点P按B→C→D→A方向运动，开始时，以每秒2个单位长度匀速运动，到达C点后，改为每秒a个单位匀速运动，到达D后，改为每秒b个单位匀速运动，在整个运动过程中，三角形ABP的面积S与运动时间t的函数关系如图所示。
求：
（1）AB、BC的长；
（2）a，b的值。