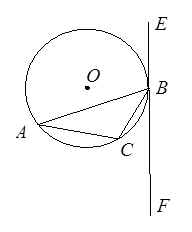在等腰 中, ,以 为直径的 分别与 , 相交于点 , ,过点 作 ,垂足为点 .
(1)求证: 是 的切线;
(2)分别延长 , ,相交于点 , , 的半径为6,求阴影部分的面积.

先化简,再求值: ,其中x是方程
,其中x是方程 的根.
的根.
解不等式组:
如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线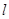 //BC,交直线CD于点F.将直线
//BC,交直线CD于点F.将直线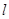 向右平移,设平移距离BE为
向右平移,设平移距离BE为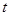 (t
(t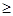 0),直角梯形ABCD被直线
0),直角梯形ABCD被直线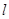 扫过的面积(图中阴影部份)为S,S关于
扫过的面积(图中阴影部份)为S,S关于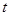 的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.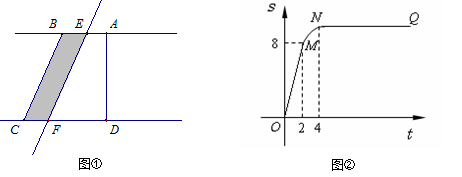
信息读取
(1)梯形上底的长AB=;
(2)直角梯形ABCD的面积=;
图象理解
(3)写出图②中射线NQ表示的实际意义;
(4)当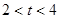 时,求S关于
时,求S关于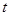 的函数关系式;
的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.
某照明有限公司研制出一种新型节能灯,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.
(1)求出月销售量y(万件)与销售单价x(元)之间的函数关系式(不必写出x的取值范围);
(2)求出月销售利润z(万元)与销售单价x(元)之间的函数关系式(不必写出x的取值范围),并求出销售单价x(元)为多少可获得最大月销售利润。(注:利润=售价-成本价)
(3)请你通过(2)中的函数关系式及其大致图象帮助公司确定产品的销售单价范围,使月销售利润不低于480万元.
已知:△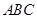 内接于⊙
内接于⊙ ,过点
,过点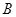 作直线
作直线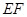 ,
, 为非直径的弦,且
为非直径的弦,且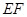 是⊙
是⊙ 的切线。(1)求证:∠CBF=∠A;(2)若
的切线。(1)求证:∠CBF=∠A;(2)若 ,BC=2,连接OC并延长交EF于点M,求由弧BC、线段BM和CM所围成的图形的面积.
,BC=2,连接OC并延长交EF于点M,求由弧BC、线段BM和CM所围成的图形的面积.