如图,在平面直角坐标系中,抛物线 与 轴交于 , 两点,与 轴交于点 ,点 是该抛物线的顶点.
(1)求抛物线的解析式和直线 的解析式;
(2)请在 轴上找一点 ,使 的周长最小,求出点 的坐标;
(3)试探究:在拋物线上是否存在点 ,使以点 , , 为顶点, 为直角边的三角形是直角三角形?若存在,请求出符合条件的点 的坐标;若不存在,请说明理由.

如图,点D,E分别在AC,AB上.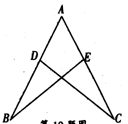
(1) 已知,BD=CE,CD=BE,求证:AB=AC;
(2) 分别将“BD=CE”记为①,“CD=BE” 记为②,“AB=AC”记为③.添加条件①、③,以②为结论构成命题1,添加条件②、③以①为结论构成命题2.命题1是命题2的命题,命题2是
命题.(选择“真”或“假”填入空格).
已知:△ABC≌△A′B′C′,AD、A′D′分别是对应边BC和B′C′边上的高。
求证:AD=A′D′。
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
求证:BC∥EF.
已知:如图,四边形ABCD中,AB∥CD ,AD∥BC。
求证:△ABD≌△CDB。
已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.
求证:AB=DC