为进一步深化基础教育课程改革,构建符合素质教育要求的学校课程体系,某学校自主开发了 书法、 阅读, 足球, 器乐四门校本选修课程供学生选择,每门课程被选到的机会均等.
(1)学生小红计划选修两门课程,请写出她所有可能的选法;
(2)若学生小明和小刚各计划选修一门课程,则他们两人恰好选修同一门课程的概率为多少?
如图,已知:抛物线C1: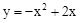 ,将抛物线C1向上平移m个单位(m>0)得抛物线C2,C2的顶点为G,与y轴交于M,点N是M关于x轴的对称点,点P(
,将抛物线C1向上平移m个单位(m>0)得抛物线C2,C2的顶点为G,与y轴交于M,点N是M关于x轴的对称点,点P(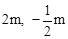 )在直线MG上。问:当m为何值时,在抛物线C2上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?
)在直线MG上。问:当m为何值时,在抛物线C2上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?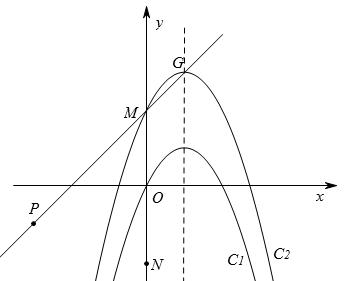
如图,在平面直角坐标系中,二次函数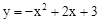 的图象与y轴交于点C,点P是抛物线上的一个动点,点P关于y轴的对称点Q,连接PO,PC,QO,QC,得到四边形
的图象与y轴交于点C,点P是抛物线上的一个动点,点P关于y轴的对称点Q,连接PO,PC,QO,QC,得到四边形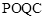 ,是否存在点P,使四边形
,是否存在点P,使四边形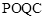 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由。
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由。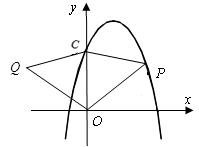
如图, 在Rt△ABC中,∠C=90º, AC=9,BC=12,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ. 点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).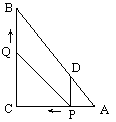
(1)直接用含t的代数式分别表示:QB=__________, PD=___________;
(2)是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由;
(3)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻成为菱形,求点Q的速度.
如图,在直角坐标系中,点A的坐标为(8,0),点B(t,b)在直线y=b上运动,点D、E、F分别为OB、OA、AB的中点,其中b是大于零的常数。设直线y=b与y轴交于点C,问:四边形DEFB能不能是矩形?若能,求出t的值;若不能,说明理由。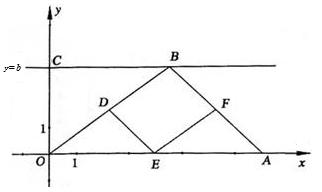
如图,已知点P是抛物线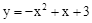 上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC=
上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC=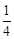 MP,MD=
MP,MD=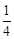 OM,OE=
OM,OE=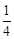 ON,NF=
ON,NF=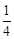 NP.问:在抛物线上是否存在这样的点P,使四边形CDEF为矩形?若存在,请求出所有符合条件的P点坐标;若不存在,请说明理由.
NP.问:在抛物线上是否存在这样的点P,使四边形CDEF为矩形?若存在,请求出所有符合条件的P点坐标;若不存在,请说明理由.