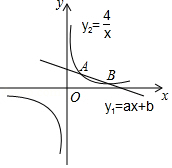
如图1,经过原点 的抛物线 、 为常数, 与 轴相交于另一点 .直线 在第一象限内和此抛物线相交于点 ,与抛物线的对称轴相交于点 .
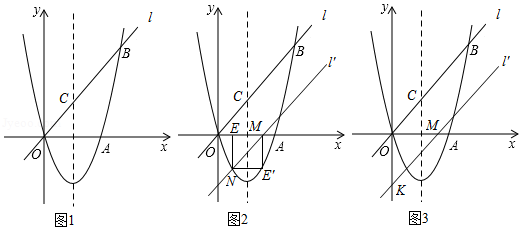
(1)求抛物线的解析式;
(2)在 轴上找一点 ,使以点 、 、 为顶点的三角形与以点 、 、 为顶点的三角形相似,求满足条件的点 的坐标;
(3)直线 沿着 轴向右平移得到直线 , 与线段 相交于点 ,与 轴下方的抛物线相交于点 ,过点 作 轴于点 .把 沿直线 折叠,当点 恰好落在抛物线上时(图 ,求直线 的解析式;
(4)在(3)问的条件下(图 ,直线 与 轴相交于点 ,把 绕点 顺时针旋转 得到△ ,点 为直线 上的动点.当△ 为等腰三角形时,求满足条件的点 的坐标.
阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
|
组别 |
时间(小时) |
频数(人数) |
频率 |
|
|
|
6 |
0.15 |
|
|
|
|
0.3 |
|
|
|
10 |
0.25 |
|
|
|
8 |
|
|
|
|
4 |
0.1 |
|
合计 |
1 |
请根据图表中的信息,解答下列问题:
(1)表中的 , ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3) 组的4人中,有1名男生和3名女生,该校计划在 组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.

如图1,抛物线 与 轴交于点 , .与 轴交于点 .连接 , .已知 的面积为2.
(1)求抛物线的解析式;
(2)平行于 轴的直线与抛物线从左到右依次交于 , 两点.过 , 向 轴作垂线,垂足分别为 , .若四边形 为正方形,求正方形的边长;
(3)如图2,平行于 轴的直线交抛物线于点 ,交 轴于点 .点 是抛物线上 , 之间的一动点,且点 不与 , 重合,连接 交 于点 .连接 并延长交 于点 .在点 运动过程中, 是否为定值?若是,求出这个定值;若不是,请说明理由.

如图,在 中,弦 与直径 垂直,垂足为 , 的延长线上有
一点 ,满足 .过点 作 ,交 的延长线于点 ,连接 交 于点 .
(1)求证: 是 的切线;
(2)如果 , ,求 的值;
(3)如果 ,求证: .

推进农村土地集约式管理,提高土地的使用效率是新农村建设的一项重要举措.某村在小城镇建设中集约了2400亩土地,计划对其进行平整.经投标,由甲乙两个工程队来完成平整任务.甲工程队每天可平整土地45亩,乙工程队每天可平整土地30亩.已知乙工程队每天的工程费比甲工程队少500元,当甲工程队所需工程费为12000元,乙工程队所需工程费为9000元时,两工程队工作天数刚好相同.
(1)甲乙两个工程队每天各需工程费多少元?
(2)现由甲乙两个工程队共同参与土地平整,已知两个工程队工作天数均为正整数,且所有土地刚好平整完,总费用不超过110000元.
①甲乙两工程队分别工作的天数共有多少种可能?
②写出其中费用最少的一种方案,并求出最低费用.
如图,一次函数 与反比例函数 的图象交于 、 两点.点 的横坐标为2,点 的纵坐标为1.
(1)求 , 的值.
(2)在反比例 第三象限的图象上找一点 ,使点 到直线 的距离最短,求点 的坐标.