图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口 宽3.9米,门卫室外墙 上的 点处装有一盏路灯,点 与地面 的距离为3.3米,灯臂 长为1.2米(灯罩长度忽略不计), .

(1)求点 到地面的距离;
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏 保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据: ,结果精确到0.01米)
某网店销售甲、乙两种防雾霾口罩,已知甲种口罩每袋的售价比乙种口罩多5元,小丽从该网店网购2袋甲种口罩和3袋乙种口罩共花费110元.
(1)该网店甲、乙两种口罩每袋的售价各多少元?
(2)根据消费者需求,网店决定用不超过10000元购进甲、乙两种口罩共500袋,且甲种口罩的数量大于乙种口罩的 ,已知甲种口罩每袋的进价为22.4元,乙种口罩每袋的进价为18元,请你帮助网店计算有几种进货方案?若使网店获利最大,应该购进甲、乙两种口罩各多少袋,最大获利多少元?
已知 与 是两个大小不同的等腰直角三角形.
(1)如图①所示,连接 , ,试判断线段 和 的数量和位置关系,并说明理由;
(2)如图②所示,连接 ,将线段 绕 点顺时针旋转 到 ,连接 ,试判断线段 和 的数量和位置关系,并说明理由.

某学校教学楼(甲楼)的顶部 和大门 之间挂了一些彩旗.小颖测得大门 距甲楼的距离 是 ,在 处测得甲楼顶部 处的仰角是 .
(1)求甲楼的高度及彩旗的长度;(精确到
(2)若小颖在甲楼楼底 处测得学校后面医院楼(乙楼)楼顶 处的仰角为 ,爬到甲楼楼顶 处测得乙楼楼顶 处的仰角为 ,求乙楼的高度及甲乙两楼之间的距离.(精确到
, , , , ,

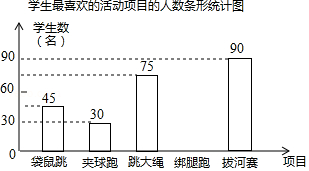
为了丰富校园文化,某学校决定举行学生趣味运动会,将比赛项目确定为袋鼠跳、夹球跑、跳大绳、绑腿跑和拔河赛五种,为了解学生对这五项运动的喜欢情况,随机调查了该校 名学生最喜欢的一种项目(每名学生必选且只能选择五项中的一种),并将调查结果绘制成如图不完整的统计图表:
学生最喜欢的活动项目的人数统计表
|
项目 |
学生数(名 |
百分比 |
|
袋鼠跳 |
45 |
15 |
|
夹球跑 |
30 |
|
|
跳大绳 |
75 |
25 |
|
绑腿跑 |
|
20 |
|
拔河赛 |
90 |
30 |
根据图表中提供的信息,解答下列问题:
(1) , , .
(2)请将条形统计图补充完整;
(3)根据调查结果,请你估计该校3000名学生中有多少名学生最喜欢绑腿跑;
(4)根据调查结果,某班决定从这五项(袋鼠跳、夹球跑、跳大绳、绑腿跑和拔河赛可分别记为 、 、 、 、 中任选其中两项进行训练,用画树状图或列表的方法求恰好选到学生喜欢程度最高的两项的概率.
定义:点 是 内部或边上的点(顶点除外),在 , , 中,若至少有一个三角形与 相似,则称点 是 的自相似点.
例如:如图1,点 在 的内部, , ,则 ,故点 是 的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点 是曲线 上的任意一点,点 是 轴正半轴上的任意一点.
(1)如图2,点 是 上一点, ,试说明点 是 的自相似点;当点 的坐标是 , ,点 的坐标是 , 时,求点 的坐标;
(2)如图3,当点 的坐标是 ,点 的坐标是 时,求 的自相似点的坐标;
(3)是否存在点 和点 ,使 无自相似点?若存在,请直接写出这两点的坐标;若不存在,请说明理由.
