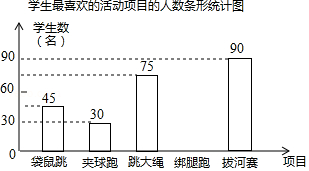
为了丰富校园文化，某学校决定举行学生趣味运动会，将比赛项目确定为袋鼠跳、夹球跑、跳大绳、绑腿跑和拔河赛五种，为了解学生对这五项运动的喜欢情况，随机调查了该校 名学生最喜欢的一种项目（每名学生必选且只能选择五项中的一种），并将调查结果绘制成如图不完整的统计图表：
学生最喜欢的活动项目的人数统计表
项目 |
学生数（名 |
百分比 |
袋鼠跳 |
45 |
15 |
夹球跑 |
30 |
|
跳大绳 |
75 |
25 |
绑腿跑 |
|
20 |
拔河赛 |
90 |
30 |
根据图表中提供的信息，解答下列问题：
（1） ， ， ．
（2）请将条形统计图补充完整；
（3）根据调查结果，请你估计该校3000名学生中有多少名学生最喜欢绑腿跑；
（4）根据调查结果，某班决定从这五项（袋鼠跳、夹球跑、跳大绳、绑腿跑和拔河赛可分别记为 、 、 、 、 中任选其中两项进行训练，用画树状图或列表的方法求恰好选到学生喜欢程度最高的两项的概率．
已知a2=1，|a|=﹣a，求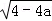
的值．
一辆汽车从A地驶往B地，前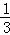
路段为普通公路，其余路段为高速公路．已知汽车在普通公路上行驶的速度为60km/h，在高速公路上行驶的速度为100km/h，汽车从A地到B地一共行驶了2.2h．
请你根据以上信息，就该汽车行驶的“路程”或“时间”，提出一个用二元一次方程组解决的问题，并写出解答过程．
某社区要调查社区居民双休日的学习状况，采用下列调查方式：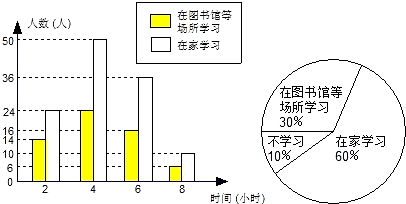
①从一幢高层住宅楼中选取200名居民；
②从不同住宅楼中随机选取200名居民；
③选取社区内200名在校学生．
（1）上述调查方式最合理的是 ；
（2）将最合理的调查方式得到的数据制成扇形统计图（如图1）和频数分布直方图（如图2），在这个调查中，200名居民双休日在家学习的有 人；
（3）请估计该社区2 000名居民双休日学习时间不少于4小时的人数．
如图，AB⊥EF，垂足为B，CD⊥EF，垂足为D，∠1=∠F，试判断∠2与∠3是否相等？并说明理由．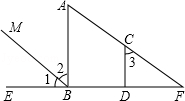
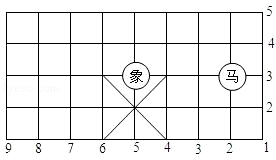
如图，“马”所处的位置为（2，3），其中“马”走的规则是沿着“日”字形的对角线走．
（1）用坐标表示图中“象”的位置是 ．
（2）写出“马”下一步可以到达的所有位置的坐标．