自我省深化课程改革以来,铁岭市某校开设了: .利用影长求物体高度, .制作视力表, .设计遮阳棚, .制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.
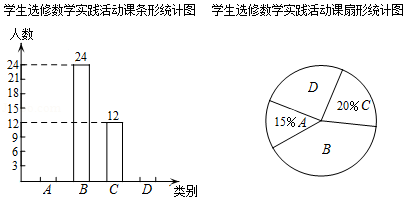
根据图中信息解决下列问题:
(1)本次共调查 名学生,扇形统计图中 所对应的扇形的圆心角为 度;
(2)补全条形统计图;
(3)选修 类数学实践活动的学生中有2名女生和2名男生表现出色,现从4人中随机抽取2人做校报设计,请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率.
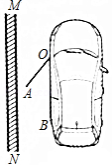
如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧 与墙 平行且距离为0.8米.已知小汽车车门宽 为1.2米,当车门打开角度 为 时,车门是否会碰到墙?请说明理由.(参考数据: ; ;
在直角坐标系中,过原点 及点 , 作矩形 、连接 ,点 为 的中点,点 是线段 上的动点,连接 ,作 ,交 于点 ,连接 .已知点 从 点出发,以每秒1个单位长度的速度在线段 上移动,设移动时间为 秒.
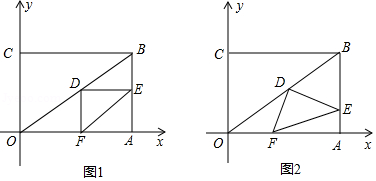
(1)如图1,当 时,求 的长.
(2)如图2,当点 在线段 上移动的过程中, 的大小是否发生变化?如果变化,请说明理由;如果不变,请求出 的值.
(3)连接 ,当 将 分成的两部分的面积之比为 时,求相应的 的值.
问题背景
如图1,在正方形 的内部,作 ,根据三角形全等的条件,易得 ,从而得到四边形 是正方形.
类比探究
如图2,在正 的内部,作 , , , 两两相交于 , , 三点 , , 三点不重合)

(1) , , 是否全等?如果是,请选择其中一对进行证明.
(2) 是否为正三角形?请说明理由.
(3)进一步探究发现, 的三边存在一定的等量关系,设 , , ,请探索 , , 满足的等量关系.
定义:如图1,抛物线 与 轴交于 , 两点,点 在该抛物线上 点与 、 两点不重合),如果 的三边满足 ,则称点 为抛物线 的勾股点.

(1)直接写出抛物线 的勾股点的坐标.
(2)如图2,已知抛物线 与 轴交于 , 两点,点 是抛物线 的勾股点,求抛物线 的函数表达式.
(3)在(2)的条件下,点 在抛物线 上,求满足条件 的 点(异于点 的坐标.
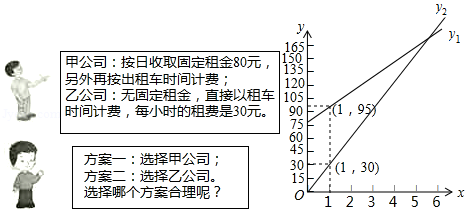
“五 一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以下信息,解答下列问题:
(1)设租车时间为 小时,租用甲公司的车所需费用为 元,租用乙公司的车所需费用为 元,分别求出 , 关于 的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算.