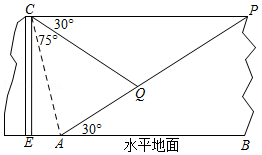
如图，某地质公园中有两座相邻小山．游客需从左侧小山山脚E处乘-优题课

题文

如图，某地质公园中有两座相邻小山．游客需从左侧小山山脚 $E$ 处乘坐竖直观光电梯上行100米到达山顶 $C$ 处，然后既可以沿水平观光桥步行到景点 $P$ 处，也可以通过滑行索道到达景点 $Q$ 处，在山顶 $C$ 处观测坡底 $A$ 的俯角为 $75 °$ ，观测 $Q$ 处的俯角为 $30 °$ ，已知右侧小山的坡角为 $30 °$ （图中的点 $C$ ， $E$ ， $A$ ， $B$ ， $P$ ， $Q$ 均在同一平面内，点 $A$ ， $Q$ ， $P$ 在同一直线上）

（1）求 $∠ CAP$ 的度数及 $CP$ 的长度；

（2）求 $P$ ， $Q$ 两点之间的距离．（结果保留根号）

科目数学题型解答题难度中等

知识点：解直角三角形的应用-仰角俯角问题

登录免费查看答案和解析

相关试题

某所学校位于北纬21°，此地一年中冬至日正午时刻，太阳光与地面的夹角最小，约为35．5°；夏至日正午时刻，太阳光的夹角最大，约为82．5°．己知该校一教学楼窗户朝南，窗高207cm，如图（1）．请你为该窗户设计一个直角形遮阳棚BCD，如图（2），要求最大限度地节省材料，夏至日正午刚好遮住全部阳光，冬至日正午能射入室内的阳光没有遮挡．

（1）在图（3）中画出设计草图；
（2）求BC、CD的长度（结果精确到个位）
（参考数据：sin35．5°≈0．58，cos35．5°≈0．81，tan35．5°≈0．71，sin82．5°≈0．99，cos82．5°≈0．13，tan82．5°≈7．60）

如图，在△ABC中，∠ABC=90°，以AB为直径的⊙O与AC边交于点D，过点D的直线交BC边于点E，∠BDE=∠A．

（1）判断直线DE与⊙O的位置关系，并说明理由．
（2）若⊙O的半径R=5，tanA=，求线段CD的长．

2014年5月12日，国家统计局公布了《2013年农民工监测调查报告》，报告显示：我国农民工收入持续快速增长．某地区农民工人均月收入增长率如图1，并将人均月收入绘制成如图2的不完整的条形统计图．

根据以上统计图解答下列问题：
（1）求2013年农民工人均月收入的增长率是多少？
（2）求2011年农民工人均月收入是多少？
（3）小明看了统计图后说：“农民工2012年的人均月收入比2011年的少了．”你认为小明的说法正确吗？请说明理由．

四张背面完全相同的纸牌（如图，用①、②、③、④表示），正面分别写有四个不同的条件．小明将这4张纸牌背面朝上洗匀后，先随机抽出一张（不放回），再随机抽出一张．

（1）写出两次摸牌出现的所有可能的结果（用①、②、③、④表示）；
（2）以两次摸出的牌面上的结果为条件，求能判断四边形ABCD为平行四边形的概率．

如图，在平面直角坐标系xOy中，已知四边形DOBC是矩形，且D（0，4），B（6，0）．若反比例函数y=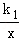（x＞0）的图象经过线段OC的中点A，交DC于点E，交BC于点F．设直线EF的解析式为y=k₂x+b．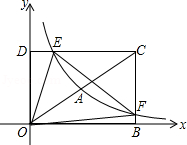

（1）求反比例函数和直线EF的解析式；
（2）求△OEF的面积；
（3）请结合图象直接写出不等式k₂x+b﹣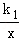＞0的解集．

试卷网试题网古诗词网作文网范文网