如图,抛物线 交 轴于点 和点 ,交 轴于点 .
(1)求这个抛物线的函数表达式.
(2)点 的坐标为 ,点 为第二象限内抛物线上的一个动点,求四边形 面积的最大值.
(3)点 为抛物线对称轴上的点,问:在抛物线上是否存在点 ,使 为等腰直角三角形,且 为直角?若存在,请直接写出点 的坐标;若不存在,请说明理由.

如图所示,在△ABC中,D是AC上的一点.若AB=6,AC=9,AD=4,判断△ABD与△ACB是否相似.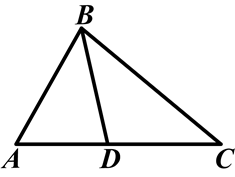
已知△ABC与△A′B′C′均为直角三角形,且∠C=∠C′=90°,AB=10cm,BC=6cm,A′B′=5cm,B′C′=3cm,那么△ABC∽△A′B′C′吗?
如图,若∠1=∠2,则图中有哪些三角形相似?分别把它们写出来,并说明理由.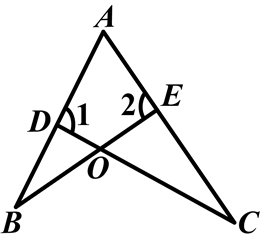
如图,已知AB=1cm,BD=2cm,AC=2cm,CE=4cm,△ABC与△ADE是否相似?请说明理由.
下面给出△ABC和△DEF的各条边长,是否能判定△ABC∽△DEF?为什么?
(1)AB=3cm,BC=4cm,AC=5cm,DE=1.5cm,EF=2cm,DF=3cm;
(2)AB=4cm,BC=7cm,AC=5cm,DE=2cm,EF=3.5cm,DF=2.5cm;
(3)AB=8cm,BC=10cm,AC=9cm,DE=10cm,EF=25cm.DF=18cm.