如图, 内接于 , 与 是 的直径,延长线段 至点 ,使 ,连接 交 于点 , 交 于点 .
(1)求证: 与 相切.
(2)若 , ,求扇形 的面积.

如图, 一座钢结构桥梁的框架是 ,水平横梁 长 18 米, 中柱 高 6 米, 其中 是 的中点, 且 .
(1) 求 的值;
(2) 现需要加装支架 、 ,其中点 在 上, ,且 ,垂足为点 ,求支架 的长 .
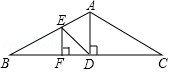
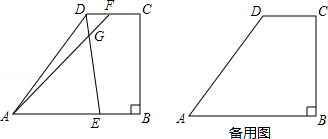
如图所示,梯形 中, , , , , ,点 是边 上的动点,点 是射线 上一点,射线 和射线 交于点 ,且 .
(1)求线段 的长;
(2)如果 是以 为腰的等腰三角形,求线段 的长;
(3)如果点 在边 上(不与点 、 重合),设 , ,求 关于 的函数解析式,并写出 的取值范围.
如图,抛物线 经过点 ,与 轴的负半轴交于点 ,与 轴交于点 ,且 ,抛物线的顶点为点 .
(1)求这条抛物线的表达式;
(2)联结 、 、 、 ,求四边形 的面积;
(3)如果点 在 轴的正半轴上,且 ,求点 的坐标.

已知:如图, 是 的外接圆, ,点 在边 上, , .
(1)求证: ;
(2)如果点 在线段 上(不与点 重合),且 ,求证:四边形 是平行四边形.

某物流公司引进 、 两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时, 种机器人于某日0时开始搬运,过了1小时, 种机器人也开始搬运,如图,线段 表示 种机器人的搬运量 (千克)与时间 (时 的函数图象,线段 表示 种机器人的搬运量 (千克)与时间 (时 的函数图象.根据图象提供的信息,解答下列问题:
(1)求 关于 的函数解析式;
(2)如果 、 两种机器人连续搬运5个小时,那么 种机器人比 种机器人多搬运了多少千克?
