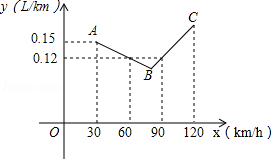
如图中的折线 表示某汽车的耗油量 (单位: 与速度 (单位: 之间的函数关系 ,已知线段 表示的函数关系中,该汽车的速度每增加 ,耗油量增加 .
(1)当速度为 、 时,该汽车的耗油量分别为 、 .
(2)求线段 所表示的 与 之间的函数表达式.
(3)速度是多少时,该汽车的耗油量最低?最低是多少?
某校进行期末体育达标测试,甲、乙两班的学生数相同,甲班有48人达标,乙班有45人达标,甲班的达标率比乙班高 ,求乙班的达标率.
解不等式组,并把解集表示在数轴上.
.
(1)已知: 是等腰三角形,其底边是 ,点 在线段 上, 是直线 上一点,且 ,若 (如图①).求证: ;
(2)若将(1)中的“点 在线段 上”改为“点 在线段 的延长线上”,其它条件不变(如图②),(1)的结论是否成立,并说明理由;
(3)若将(1)中的“若 ”改为“若 ”,其它条件不变,则 的值是多少?(直接写出结论,不要求写解答过程)

如图,在平面直角坐标系中,抛物线 的顶点坐标为 ,与 轴交于点 ,与 轴交于点 、 .
(1)求二次函数 的表达式;
(2)过点 作 平行于 轴,交抛物线于点 ,点 为抛物线上的一点(点 在 上方),作 平行于 轴交 于点 ,问当点 在何位置时,四边形 的面积最大?并求出最大面积;
(3)若点 在抛物线上,点 在其对称轴上,使得以 、 、 、 为顶点的四边形是平行四边形,且 为其一边,求点 、 的坐标.

某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元 个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.